CS 660: Combinatorial Algorithms
( a, b ) Trees
[To Lecture Notes Index]
San Diego State University -- This page last updated October 21, 1995
Leaf-Oriented Storage
All items of interest are stored in the leafs
Leaf contains one key
Internal nodes contain keys used to find leafs
Let a and b be integers with a >= 2 and 2a-1 <= b. A tree T is an
(a,b)-tree if
a) All leaves of T have the same depth
b) All internal nodes v of T satisfy c(v) <= b
c) All internal nodes v of T except the root satisfy c(v) >= a
d) The root of T satisfies c(v) >= 2
c(v) = number of children of node v
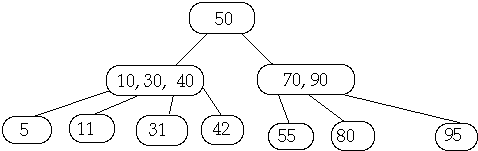
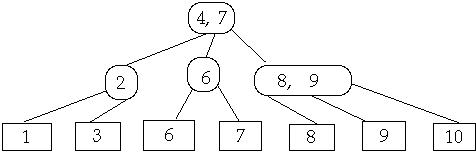
Insertion in (2,4) Tree, Insert 6
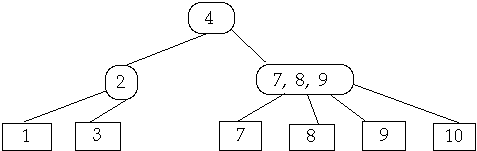
Find Proper Leaf Location and Add
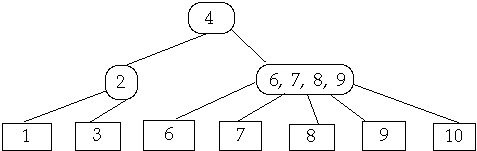
If needed Split Node
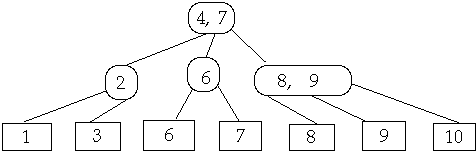
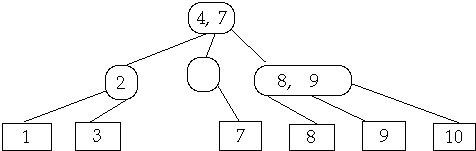
Delete 6
Find and Delete leaf, Shrink Parent
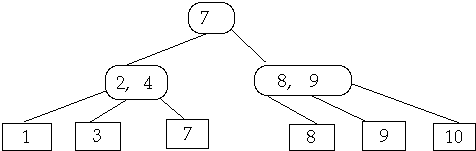
If needed either fuse parent or
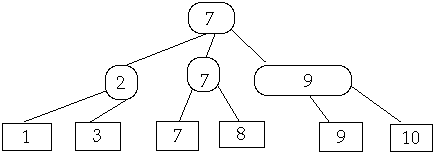
Share nodes from Sibling
Let T be an ( a, b )-tree with n leaves and height h. Then:
a)
b) lg (n)/lg (b) <= h <= 1 + lg( n/2 ) / log ( a )
Theorem[1] Let b >= 2a and
a >= 2. Perform any sequence of i insertions and d deletions( n = i + d )
into an initially empty ( a, b)-tree. Let
- SP = total number of node splittings
- F = total number of node fusings
- SH = total number of node sharings
then:
- SH <= d <= n
-
- (2c - 1) SP + cF <= n + c + c (i - d - 2) / ( a + c - 1 )
where:
-
Note c >= 1 so we have SP + F <= n/c + 1 + (n - 2 ) / a
Corollary SP + F + SH = O( n ).
This is not true when b = 2a - 1. That is for B-trees!
Values of a and b?
Assume b = 2a
Assume it costs C1 + C2m time units to move m contiguous elements from
secondary to main memory
C1 = latency time, C2 = time to move one storage location
Assume it costs K1 + K2n to determine the subtree of interest in a node
containing n keys
Total search time in (a , b ) -tree will be bound by
- ( K1 + K2a + C1 + C2a ) lg( n ) / lg( a )
This is minimal when
- a* ln( a - 1 ) = ( K1 + C1 ) / ( K2 + C2 )
Tree In Main Memory
K1 ~ K2 ~ C1 and C2 = 0 so a = 2 or 3
Tree In Secondary Memory
K1 ~ K2 ~ C2 and C1 ~ 1000K1 ( in 1983 )
This gives a ~ 100
The Action is Near the Leaves
Let leaves be level 0
Parents of leaves be level 1, ...
Theorem[2] Let b >= 2a and
a >= 2. Perform any sequence of i insertions and d deletions( n = i + d )
into an initially empty ( a, b)-tree. Let
- SPh = total number of node splittings at height h
- Fh = total number of node fusings at height h
- SHh = total number of node sharings at height h
then:
- SPh + SHh + Fh <= 2( c + 2 ) n / (c + 1 ) h
-
where:
( a, b )-Trees and Sorting
Let x[1], x[2], ..., x[n] be a sequence to be sorted
f[i] = | { x[j] : j > k and x[j] < x[k] } |
Let
F is the number of inversions of x[1], x[2], ..., x[n]
Sort x[1], x[2], ..., x[n] by inserting into a ( a, b )-Tree
But start insertions at the leaves.
theorem A sequence of n elements with F inversions can be sorted in:
- O( n + n lg( F / n ) )