CS 662 Theory of Parallel Algorithms
Past Exams
[To Lecture Notes Index]
San Diego State University -- This page last updated February 20, 1996, 1996
Contents of Past Exams
- 1993-94
- Final
- 1994-95
- Midterm
- Final
1. Produce the dag with minimal depth that will evaluate 3x**8 +
5x**4 + 7x**2 + 2.
2. Explain how to evaluate the polynomial y = b1x**(n-1) +
b2x**(n-2) + ... + bn-1x + bn for a given x using the scan
operator.
3a. Describe the odd-even transposition sort on a linear array of processors.
b. What is the time complexity and speedup of the sort if N = P. When N <
P?
4. We have N processors. Each processor flips a fair coin. Use the Chernoff
bounds to produce an upper bound on the probability that N/4 or fewer of the
processor's coin landed heads up?
5. Reduce the following to a first-order recurrence relation.
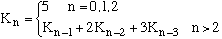
6. Explain how to compute in parallel A**-1 when A is a lower
triangular matrix. How many processors are required? How long will it
take?
7. Show how to solve for x when Ax = b using the characteristic polynomial of
a matrix.
8. Give an algorithm to compute the rank of items in a linked list. Show how
to avoid any concurrent reads or writes.
9. Explain why it is not possible to embed a complete binary tree with
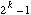nodes in a Hypercube with
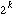nodes.
Answer any 8 of the following questions. Clearly indicate which 8 problems you
wish to be graded.
1) State Amdahl's Law. Explain the law's consequences for massively parallel
algorithms.
2) Given an algorithm of size N, optimal sequential time complexity A(N) and P
processors, can we obtain a speedup greater than P? Explain your answer.
3) Give an algorithm to lexically compare strings of N characters in parallel.
Give the time complexity of the algorithm.
4) Reduce the following to a first-order recurrence relation.
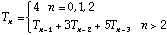
5) What are the important parameters (or characteristics) of a connection
network. Give the values of the parameters for the hypercube and the
shuffle-exchange networks.
6) What is the slow-down principle? Give an example. That is explain the
effects of the slow-down principle on an algorithm covered in the course.
7) Explain the operation of guarded commands in SR.
8) Explain how to simulate the PRAM in SR.
9) Explain how to simulate a MIMD machine in SR.
10) Explain the operation of a semaphore. Why are semaphores not used in
parallel programs?
11) Give an algorithm to broadcast an item on a hypercube.
12) Contrast the send and call operations in SR.
Answer any 8 of the following questions. Clearly indicate which 8 problems you
wish to be graded.
1. Explain why it is not possible to embed a complete binary tree with
nodes, (for k >= 6), in a mesh of any size.
2. Give a parallel algorithm to find a root of an equation of one variable.
What is the time complexity and the cost of the algorithm.
3. Give a situation where N processors connected together as a binary tree will
perform better than N processors connected as a mesh. Explain your answer.
4. Explain how to use the characteristic polynomial to compute A-1
where A is an N*N matrix.
5. We are on a CREW machine. We have P processors, a list, A[1], ... A[N], of
N integers in random order, and b buckets, B[1], ..., B[b], into which we are
to place the elements of the list. We have a sorted list of b-1 numbers S[1],
S[2], ..., S[b-1]. Bucket B[j] (j = 2, ..., b-1) gets all elements of the list
that are greater than S[j-1] and less than or equal to S[j]. Bucket B[1] gets
all elements of the list less than or equal to S[1]. Bucket B[b] gets all
numbers greater than S[b]. Give an efficient parallel algorithm to place the
elements of A in the buckets.
6. a. What are the different types of computational models of parallel
computing that use shared memory?
b. Algorithm X runs on an CRCW machine with time complexity of T(N). Algorithm
X is ported to a EREW machine. What can we say about the time complexity of X
on the EREW machine? Explain.
7. Contrast the "co" and "af" statements in SR
8. Explain how semaphores can be implemented with message queues in SR.
9. Describe a parallel algorithm to find the k'th smallest item in a random
list of integers without sorting the entire list.
10. What is the difference between a Las Vegas and a Monty Carlo algorithm?
11. Describe a parallel quicksort. What is the time complexity and cost of the
algorithm?
12. Describe an O(1) sort on an CRCW machine.
13. Describe the relationship between shuffing a deck of cards to data
movements in a shuffle-exchange network.
