 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Numerical Methods part 3
[To Lecture Notes Index]
San Diego State University -- This page last updated May 2, 1996

Jacobi
Let Ax = b then we have:
-

So
-

-
-
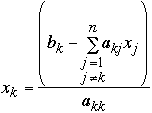
But need x's to compute x's!
Iterate
Let
 = a guess for
= a guess for
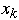
 = t'th iteration for
= t'th iteration for
 by the equation:
by the equation:
-
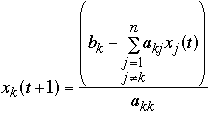
Example
 and
and
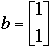
then
-

-
-
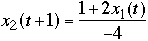
What to use for guess?
Does it work?
Two Guesses
| t | x1 | x2 | x1 | x2 |
| 0 | 0 | 0 | 1000 | 1000 |
| 1 | 0.20 | -0.3 | -599.80 | -500 |
| 2 | 0.35 | -0.4 | 300.35 | 300 |
| 3 | 0.41 | -0.4 | -179.59 | -150 |
| 4 | 0.46 | -0.5 | 90.46 | 89.5 |
| 5 | 0.47 | -0.5 | -53.53 | -45 |
| 6 | 0.49 | -0.5 | 27.49 | 26.5 |
| 7 | 0.49 | -0.5 | -15.71 | -14 |
| 8 | 0.50 | -0.5 | 8.60 | 7.6 |
| 9 | 0.50 | -0.5 | -4.36 | -4.5 |
| 10 | 0.50 | -0.5 | 2.93 | 1.93 |
| 11 | 0.50 | -0.5 | -0.96 | -1.7 |
| 12 | 0.50 | -0.5 | 1.23 | 0.23 |
| 13 | 0.50 | -0.5 | 0.06 | -0.9 |
| 14 | 0.50 | -0.5 | 0.72 | -0.3 |
| 15 | 0.50 | -0.5 | 0.37 | -0.6 |
| 16 | 0.50 | -0.5 | 0.57 | -0.4 |
| 17 | 0.50 | -0.5 | 0.46 | -0.5 |
| 18 | 0.50 | -0.5 | 0.52 | -0.5 |
| 19 | 0.50 | -0.5 | 0.49 | -0.5 |
| 20 | 0.50 | -0.5 | 0.51 | -0.5 |
Example 2
Let
 and
and
 then
then
 and
and
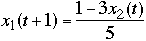
| t | x1 | x2 | x1 | x2 | x1 | x2 |
| 0 | 0 | 0 | 1 | 1 | 5 | -5 |
| 1 | 0.20 | -0.5 | -0.40 | -2.5 | 3.20 | -11 |
| 2 | 0.50 | -0.9 | 1.70 | 0.3 | 6.50 | -6.9 |
| 3 | 0.74 | -1.5 | 0.02 | -3.9 | 4.34 | -14 |
| 4 | 1.10 | -2 | 2.54 | -0.5 | 8.30 | -9.2 |
| 5 | 1.39 | -2.7 | 0.52 | -5.6 | 5.71 | -17 |
| 6 | 1.82 | -3.3 | 3.55 | -1.5 | 10.46 | -12 |
| 7 | 2.17 | -4.1 | 1.13 | -7.6 | 7.35 | -21 |
| 8 | 2.68 | -4.8 | 4.76 | -2.8 | 13.05 | -15 |
| 9 | 3.10 | -5.9 | 1.85 | -10 | 9.32 | -27 |
| 10 | 3.72 | -6.7 | 6.21 | -4.2 | 16.16 | -19 |
| 11 | 4.22 | -7.9 | 2.73 | -13 | 11.68 | -33 |
| 12 | 4.96 | -8.9 | 7.95 | -6 | 19.89 | -24 |
| 13 | 5.56 | -10 | 3.77 | -16 | 14.52 | -40 |
| 14 | 6.46 | -12 | 10.04 | -8 | 24.37 | -30 |
| 15 | 7.17 | -13 | 5.02 | -21 | 17.92 | -49 |
| 16 | 8.25 | -15 | 12.55 | -11 | 29.75 | -36 |
| 17 | 9.11 | -17 | 6.53 | -26 | 22.01 | -60 |
| 18 | 10.40 | -19 | 15.56 | -14 | 36.20 | -45 |
| 19 | 11.43 | -21 | 8.34 | -32 | 26.91 | -73 |
| 20 | 12.98 | -23 | 19.17 | -17 | 43.94 | -54 |
Convergence
When does this work?
Let D be the diagonal matrix whose diagonal entries are equal to diagonal
entries of A
Let B = A -D
Then
 can be written as
can be written as
-
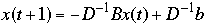
 converges to x for all initial guesses if and only if
converges to x for all initial guesses if and only if
-

This happens if and only if the eigenvalues of
 are all less than 1
are all less than 1
Def. A square matrix A with entries
 is row diagonally dominant if
is row diagonally dominant if
-
 for all j
for all j
Theorem.
- If A is row diagonally dominant than the Jacobi method converges
Example 1

Example 2

Gauss-Seidel Method
Let Ax = b and let
-
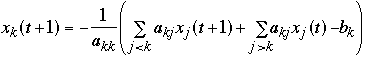
if
 converges it converges to x
converges it converges to x
Theorem
- If the Jacobi method converges for a given A then the Gauss-Seidel method
also converges
Where is the Parallelism?
Gauss-Seidel Method
-

Jacobi Method
-
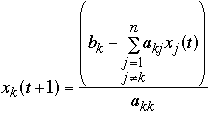


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms