 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Selection
[To Lecture Notes Index]
San Diego State University -- This page last updated March 12, 1996, 1996

Selection Problem
Let S be a list of n items in random order
Problem - Find the k'th smallest item in the list
Sequential Select
Sequential_Select( S, k ), Q is a constant
Step 1
- if | S| < Q then sort S and return k'th element
- else
- subdivide S into |S |/Q sublists of Q elements each
Step 2
- Sort each sublist and determine its median
Step 3
- Call Sequential_Select to find m, median of the |S |/Q medians found in
step 2
Step 4
- Let L = elements of S that are less than m
- Let E = elements of S that are equal to m
- Let G = elements of S that are greater than m
Step 5
- if | L | >= k then return Sequential_Select( L, k )
- if | L |+| E | >= k then return m
- return Sequential_Select( G , k -| L |-| E |)
Is it worth all the Effort?
Analysis
Define
- t(n) = time required in worst case to find the k'th smallest item in
a list of n items
Step 1
- if | S| < Q then sort S and return k'th element
- else
- subdivide S into |S |/Q sublists of Q elements each
Sorting takes constant time
Subdividing takes c1*n
-
Step 2
- Sort each sublist and determine its median
Sorting one list takes constant time
Sorting all lists takes c2*|S |/Q = c2* n
Step 3
- Call Sequential_Select to find m, median of the |S |/Q medians found in
step 2
This takes t( n / Q )
Step 4
- Let L = elements of S that are less than m
- Let E = elements of S that are equal to m
- Let G = elements of S that are greater than m
Requires one linear pass of S so takes c3* n
Step 5
- if | L | >= k then return Sequential_Select( L, k )
- if | L |+| E | >= k then return m
- return Sequential_Select( G , k -| L |-| E |)
Claim: |S|/4 items of S will be greater then or equal to m
proof:
- There are |S |/2Q medians larger then m
-
- Each median is the median of list of size Q
-
- Each median has Q/2 items larger or equal to it
-
- So there are |S |/2Q * Q/2 = |S|/4 items of S will be greater then or
equal to m
We have
- | L | <= 3*|S|/4
- | G | <= 3*|S|/4
Hence a call to Sequential_Select takes t( 3n/4) time
We have:
t( n ) = k* n + t( n / Q ) + t( 3n/4), k = c1 + c2 + c3
Need Q so that n / Q + 3n/4 < n
Any Q >= 5 will work, pick 5
t( n ) = k* n + t( n / 5 ) + t( 3n/4)
Assume that T ( n ) <= c*n
We get:
t( n ) = k* n + c* n / 5 + c* 3n/4
- = k* n + c* 19*n/20, let c = 20k
-
- = k* n + 19k*n
-
- = 20k*n = c*n
Let S be a list of n items in random order
We have N processors ( I will use P = N )
Determine x such that
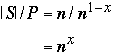
Each processor will get n/N =
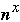 elements
elements
M is an array in shared memory
Problem - Find the k'th smallest item in the list
Parallel_Select( S, k )
Step 1
- if | S| < 5 then sort S and return k'th element
- else
- subdivide S into P sublists of |S|/P =
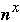 elements each
elements each
- Pi gets sublist Si
Step 2 for i = 1 to P ( =
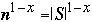 )
do in parallel
)
do in parallel
- Each processor determines mi the median of its sublist using
Sequential_Select( Si, |Si|/2 )
-
- Set M[i] = mi
Step 3 Find the median of M
- Parallel_Select( M, |M|/2 )
Step 4a
- Let Li = elements of Si that are less than m
- Let Ei = elements of Si that are equal to m
- Let Gi = elements of Si that are greater than m
Step 4b Construct L, E, G from Li, Ei, Gi, i = 1 to P
- Let L = elements of S that are less than m
- Let E = elements of S that are equal to m
- Let G = elements of S that are greater than m
-
- Perform a pre-scan on |L1|, |L2|, |L3|, ... |LP| to get
- 0, |L1|, |L1| + |L2|, |L1| + |L2| + |L3|, etc.
-
- Now processor Pi places it list Li starting in location
- |L1| + |L2| + |L3| + ... |Li-1| of array L (assuming L starts at location 0)
-
- Do the same for E and G
Step 5
- if | L | >= k then return Parallel_Select( L, k )
- if | L |+| E | >= k then return m
- return Parallel_Select( G , k -| L |-| E |)
Analysis of Parallel_Select
Define
- t(n) = time required in worst case to find the k'th smallest item in
a list of n items using Parallel_Select
Step 1
- if | S| < 5 then sort S and return k'th element
- else
- subdivide S into P sublists of |S|/P =
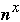 elements each
elements each
- Pi gets sublist Si
Need to broadcast |S| and address of S c1*log( P )
Sorting when | S| < 5 takes constant time
Subdividing takes constant time
-
Step 2
- Each processor determines mi the median of its sublist using
Sequential_Select( Si, |Si|/2 )
Takes c2 * |S|/P time
Step 3
- Parallel_Select( M, |M|/2 )
This takes t( P )
Step 4a
- Let Li = elements of Si that are less than m
- Let Ei = elements of Si that are equal to m
- Let Gi = elements of Si that are greater than m
Requires one linear pass of Si so takes c3* n/P
Step 4b Construct L, E, G from Li, Ei, Gi, i = 1 to P
Requires three scans (log( P )) and linear pass on Si
Takes c3 * |S|/P + c4 * log(P) time
Step 5
- if | L | >= k then return Parallel_Select( L, k )
- if | L |+| E | >= k then return m
- return Parallel_Select( G , k -| L |-| E |)
We have
- | L | <= 3*|S|/4
- | G | <= 3*|S|/4
Hence a call to Sequential_Select takes t( 3n/4) time
We have:
t( n ) = c1*log( P ) + c2 * |S|/P + t( P ) + c3 * |S|/P +
- c4 * log(P) + t( 3n/4)
But:
-
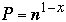
-
-
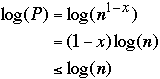
-
-
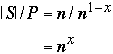
So
t( n ) = c1*log( n ) + c2 *
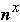 + t(
+ t(
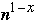 ) + c3 *
) + c3 *
 +
+
- c4 * log( n ) + t( 3n/4)
Which gives:
t( n ) = O(
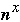 ) = O( |S|/P )
) = O( |S|/P )


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms