CS 660: Splay Tree

CS 660: Combinatorial Algorithms
Splay Tree

[To Lecture Notes Index]
San Diego State University -- This page last updated Sept 27, 1995

Contents of Splay Tree Lecture

Self-Organizing BST
1. Splay Trees

Self-Organizing BST

Basic Rotation
Simple Exchange (Transpose)

When we access a node, apply a rotation to move the node one level closer to root

If each node is accessed with probability of 1/n the average search time is:

Move-to-root

When we access a node, apply series of rotations to make the node the root

We have a list of n items: a1, a2, ..., an

Probability of accessing item ak is P(ak)

The average search cost is[1]



Where H(P(a1), ....P(an)) is the entropy of the distribution

If P(ak) = 1/n then

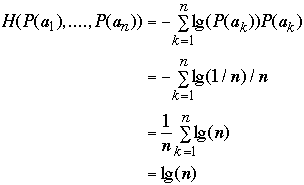
Move-to-root example

Splaying
Splay step at x

let p(x) = parent of node x

case 1 (zig) p(x) = root of the tree

case 2 (zig-zig) p(x) is not the root and x and p(x) are both left (right) children
case 3 (zig-zag) p(x) is not the root and x is a left (right) child and p(x) is a right(left ) child

To Splay a node X, repeat the splay step on X until it is the root
Splay B

Splay vs. Move-to-root
Case 1
Case 2

Splay vs. Move-to-root
Case 3

Move-to-root A

Splay A

Performance of Splay Tree

Splaying at a node of depth d takes Theta(d) time

ck= actual cost of operation k

= amortized cost of operation k

Dk = the state of the data structure after applying k'th operation to Dk

= potential associated with Dk

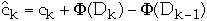
so we get:

The actual amount of work required is given by:

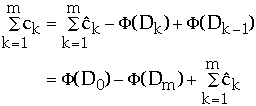
So need the total amortized work and difference in potential

Potential for Splay Trees
Let:

w(x) = weight of node x, a fixed but arbitrary value

size(x) =

rank(x) = lg(size(x))

Example
Let w(x) = 1/n where n is the number of nodes in the tree

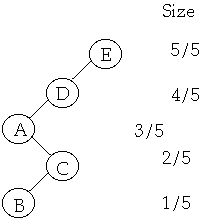
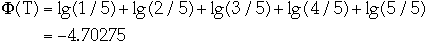
Lemma The amortized time to splay node x in a tree with root at t is at most 3(r(t) - r(x)) + 1 = O(lg(s(t)/s(x)))

Let s, r denote the size, rank functions before a splay

Let s', r' denote the size, rank functions after a splay

Count rotations

Case 1 (zig) One rotation

Amortized time of this step is:

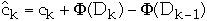
1 + [r'(x) + r'(y)] - r(x) - r(y) only x and y change rank

<= 1 + r'(x) - r(x): r(y) >= r'(y)

<= 1 + 3(r'(x) - r(x)): r'(x) >= r(x)

Case 2 (zig-zig) Two rotations

Amortized time of this step is:

2 + r'(x) + r'(y) + r'(z)
- r(x) - r(y) - r(z) only x, y ,z change rank

= 2 + r'(y) + r'(z) - r(x) - r(y): r'(x) = r(z)

<= 2 + r'(x) + r'(z) - 2r(x): r'(x) >= r'(y) and
: r(y) >= r(x)

Assume that 2r'(x) - r(x) - r'(z) >= 2

2 + r'(x) + r'(z) - 2r(x)

<= 2r'(x) - r(x) - r'(z) + r'(x) + r'(z) - 2r(x)

= 3r'(x) - 3r(x)

Need to show 2r'(x) - r(x) - r'(z) >= 2

Claim 1

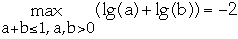
Set b = 1-a

We have

Setting this to 0 to find extreme value we get



so



that is a = 1/2 and b = 1/2

but lg(1/2)+lg(1/2)= -2

End claim 1

Claim 2 2r'(x) - r(x) - r'(z) >= 2

Recall that:



We have:
r(x) + r'(z) - 2r'(x) = lg(s(x)) + lg(s'(z)) - 2lg(s'(x)) = lg(s(x)/s'(x)) + lg(s'(z)/s'(x))

Now s(x) + s'(z) <= s'(x): (Why?)

so
0<= s(x)/s'(x) + s'(z)/s'(x) <= 1

Set s(x)/s'(x) = a and s'(z)/s'(x) =b in claim 1 to get


lg(s(x)/s'(x)) + lg(s'(z)/s'(x)) <= -2

Thus r(x) + r'(z) - 2r'(x) <= -2 or 2r'(x) - r(x) - r'(z) >= 2Case 3 (zig-zag)

Amortized time of this step is:

2 + r'(x) + r'(w) + r'(z)
- r(x) - r(w) - r(z)

<= 2 + r'(w) + r'(z) - 2r(x): r'(x) = r(z) and
: r(w) >= r(x)

Assume that 2r'(x) - r'(w) - r'(z) >= 2

2 + r'(w) + r'(z) - 2r(x) <= [2r'(x) - r'(w) - r'(z)] + r'(w) + r'(z) - 2r(x)

= 2r'(x) - 2r(x) <= 3 * ( r'(x) - r(x) )

Claim 3: 2r'(x) - r'(w) - r'(z) >= 2

Proof: see claims 1 & 2

Putting it All together
Lemma The amortized time to splay node x in a tree with root at t is at most 3(r(t) - r(x)) + 1 = O(lg(s(t)/s(x)))
Splay at B

Cost of Step 1 <= 3* ( r'(B) - r(B) ) case 3

Cost of Step 2 <= 3 * ( r''(B) - r'(B) ) case 2

Total cost = 3* ( r'(B) - r(B) ) + 3 * ( r''(B) - r'(B) )

= 3 * ( r''(B) - r(B) )

= 3 * ( r(E) - r(B) )

Case 1 only happens when splaying a child of the root

This happens at most once per splay

Amortized Cost of M Splay Operations on Tree with N nodes
Let node i be accessed q(i) times.

Then

Theorem (Balance Theorem) The total access time is

O( (m + n) * lg (n + m) )

Theorem (Static Optimality) If every item is accessed at least once, then the total access time is:

Example

Let q( i ) = 1 then we have

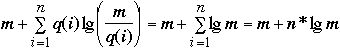
proof of Static Optimality:

Recall that:

size(x) =

rank(x) = lg(size(x))

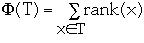
let w(i) = q(i)/m then

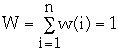
We wish to compute the actual cost of m operations.

Recall:

So we need to compute the change in potential and the amortized cost over m operations.
First the change in potential.

The biggest change in potential comes when a node moves from root to a leaf.

Assume that all nodes start at the root and end up as a leaf.

This will give us an upper bound on the change in potential.

We have:

rank of the root = lg(W)

rank of node i as a leaf = lg( w( i ) )

So change in rank of node i is at most

lg(W) - lg( w( i ) ) = lg( W/w(i) )

so the upper bound on the net decrease in potential over m operations is:

The amortized access time of item i is:

Amortized access of all times is

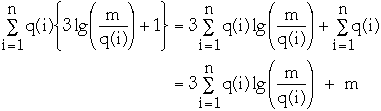
So the total cost is bounded by:

Splay Operations

access(i, t): if i is in tree t return pointer to i, otherwise return null pointer

Find i, then splay tree t at i.
If i is not in tree t, then splay last node accessed looking for i

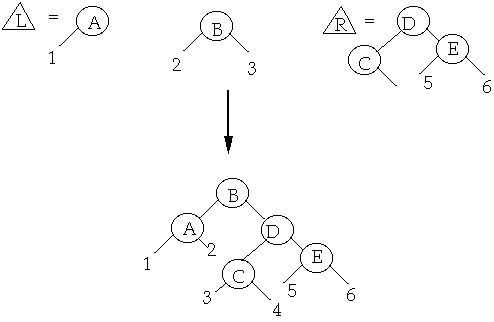
join (a, b): Return tree formed by combining tree "a", and tree "b". Assumes that every item in "a" has key less then every item in "b"

Splay largest item in "a", then add "b" as a right child of root of "a"

split (i, t): Split tree t, containing item i, into two trees: "a", containing all items with key less or equal to "i"; and "b", containing all items with key greater than "i"