CS 660: Graphs and Network Flows

CS 660: Combinatorial Algorithms
Graphs and Network Flows

[To Lecture Notes Index]
San Diego State University -- This page last updated November 16, 1995

Contents of Graphs and Network Flows Lecture

Definitions

Graph

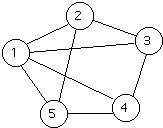
A graph G is a pair (V,E) where

V is a set of vertices (or nodes)

E is a set of edges connecting the vertices

EXAMPLE

V = {1,2,3,4,5}

E = {(1,2), (1,3), (1,4), (1,5), (2,3), (3,4), (4,5),(5,2)}

Digraph

A Digraph is a graph in which each edges has a direction.

EXAMPLE

V = { 1,2,3,4,5}

Subgraph

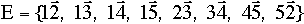
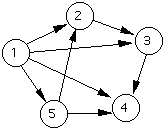
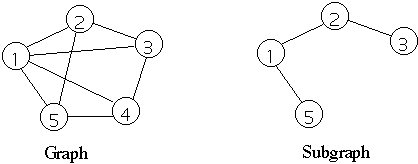
A Subgraph G'= (E',V') of a graph G = (E,V) is a graph where V' is a subset of V and E' is a subset of E

Complete Graph

A graph with an edge between each pair of vertices

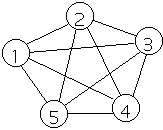
Note for any G = (E,V) we have  0 <= |E| <= |V|*(|V|-1)/2

A path in a graph from vertex V to vertex W is a sequence of edges (V1,V2), (V2,V3),... (Vk-2,Vk-1), (Vk-1,Vk) such that V = V1, and W = Vk. The path is usually given as V1,V2,V3,...Vk
The above path has length k.

Adjacent Vertices

Two vertices are adjacent if there is an edge connecting them

Connected Graph

A graph is connected if there is a path between any two vertices

Cycle

A path starting and ending on the same vertex

Simple Cycle

A cycle in which all vertices are visited exactly once except the starting vertex: which is visited only twice

Weighted Graph

A weighted graph G = (V,E,W) is a graph where each edge e in E has a weight denoted by W(e)

The weight of a Graph is the sum of the weights of the edges of the graph

Representation of Graphs

List of edges

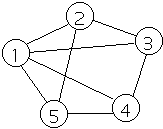
EXAMPLE

1, 2
1, 3
1, 4
1, 5
2, 3
3, 4
4, 5
5, 2

Space - O(|E|) ( actually 2|E|)

Adjacency Matrix

	1	2	3	4	5
1	0	1	1	1	1
2	1	0	1	0	1
3	1	1	0	1	0
4	1	0	1	0	1
5	1	1	0	1	0

Space - O(|V|²) (can be ~ |V|²/2)

For weighted graph

Adjacency list

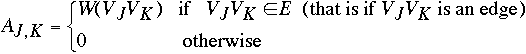
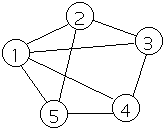
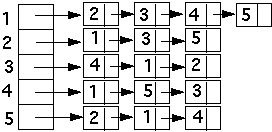
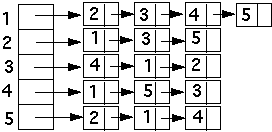
Space - O(|E| + |V|)

Incidence Matrix

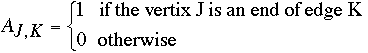
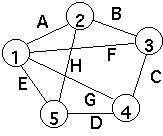
	A	B	C	D	E	F	G	H
1	1	0	0	0	1	1	1	0
2	1	1	0	0	0	0	0	1
3	0	1	1	0	0	1	0	0
4	0	0	1	1	0	0	1	0
5	0	0	0	1	1	0	0	1

Space - O(|E|*|V|)

Traversing Graphs

Breath-first(Graph, startNode)

                                  Line number
for X := 1 to |V| do                      1
	Type[X] := unvisited;                  2

Create(Queue);                             3
Type[startNode] := inQueue                 4
Insert(startNode, Queue);                  5
visitOrder := 1;                           6

while not IsEmpty(Queue) do              7
	nextNode := GetFirst(Queue);            8
	List[nextNode] := visitOrder;           9
	visitOrder := visitOrder + 1;          10
	Type[nextNode] = visited;              11
	for each node adjacent to nextNode do 12
		if Type[node] = unvisited then     13
			Type[node] := inQueue;           14
			Insert(node, Queue);             15
		end if;
	end for;
end while;

return List

Analysis of Breath-First Search

Measure of size of input: |E| and |V|
Structures used:

Type

array of size |V|
Each element changed at most three times: random -> unvisited -> inQueue -> visited

List

array of size |V|
Each element changed once

Queue

Contains at most |V| - 1 elements
At most |V| adds and |V| deletes from queue
At most |V| calls to IsEmpty

VisitOrder

Increased |V| times

Analysis of Breath-First Search - Cont.

Graph

Must find all neighbors of each node in graph

Adjacency Matrix O(|V|²)

	1	2	3	4	5
1	0	1	1	1	1
2	1	0	1	0	1
3	1	1	0	1	0
4	1	0	1	0	1
5	1	1	0	1	0

Adjacency list O(|E| + |V|)

Traversing Graphs

Depth-first(Graph, startNode)

                                  Line number
for X := 1 to |V| do                      1
	Type[X] := unvisited;                  2

Create(Stack);                             3
Type[startNode] := inStack;                4
Insert(startNode, Stack);                  5
visitOrder := 1;                           6

while not IsEmpty(Stack) do              7
	nextNode := Pop(Stack);                 8
	List[nextNode] := visitOrder;           9
	visitOrder := visitOrder + 1;          10
	Type[nextNode] = visited;              11
	for each node adjacent to nextNode do 12
		if Type[node] = unvisited then     13
			Type[node] := inStack;           14
			Push(node, Stack);               15
		end if;
	end for;
end while;

Network Flow

A flow network G = (V, E) is a directed graph where each edge (u, v) [[propersubset]] E has a capacity c(u, v) >= 0

Source (s) - node with only outflows

Sink (t) - node with only inflows

Assume graph is connected

Multiple Sources/Sinks

Super Sources and Sinks

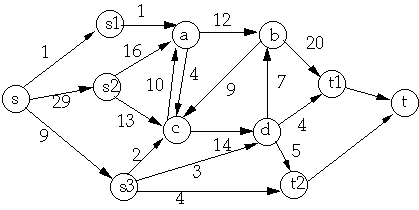
A flow in G is a real-valued function f : V * V -> R such that:

For all u, v [[propersubset]] V, f(u, v) <= c(u, v) [Capacity constraint]
For all u, v [[propersubset]] V, f(u, v) = -f(v, u) [Skew symmetry]
For all u [[propersubset]] V - {s, t}, 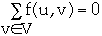[Flow conservation]

Value of a flow f is

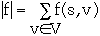
Positive Net Flow entering vertex v is

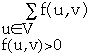
Positive Net Flow leaving vertex v is

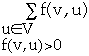
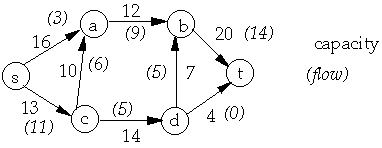
f(a, b) = 9 f(b, a) = -9 c(b, a) = 0 c(a, d) = 0 f(a, d) = 0

Oh Boy More Notation
Implicit Summation Notation

Let

then

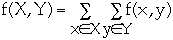
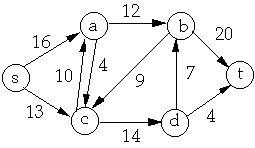
X = {a, c}, Y = {b, d } then

f(X, Y) = f(a, b) + f(a, d) + f(c, b) + f(c, b)

= 12 + 0 + -9 + 14

= 17

Lemma. Let G = (V, E) be a flow network and f be a flow in G
a. If

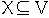then f(X, X) = 0

b. If

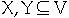then f(X, Y) = -f(Y, X)

c. If

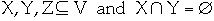then

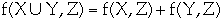and

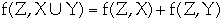
proof of a

For all u [[propersubset]] V f(u, u) = 0 since we have f(u, u) = -f(u, u)
We have:



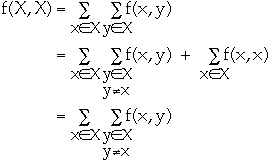
For every term f(x, y) we also have f(y, x)

Since f(x, y) = -f(y, x) we have f(X, X) = 0

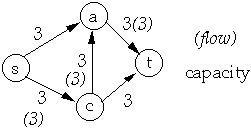
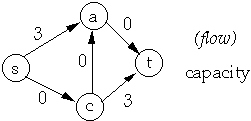
Let G = (V, E) be a flow network and f a flow in G

residual capacity of (u, v) is cf(u, v) = c(u, v) - f(u, v)

residual network of G induced by f is Gf = (V, Ef) where

Ef = { (u, v) V * V : cf(u, v) > 0}

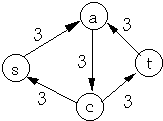
Residual Network

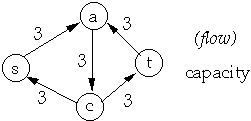
Network	Flow on Network

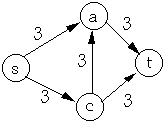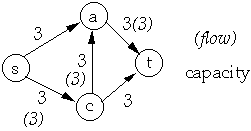Residual Network	Flow in Residual Network

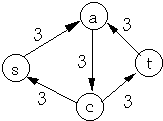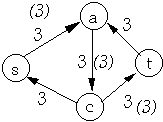Resultant Flow in Original Network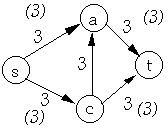

Let G = (V, E) be a flow network and f be a flow in G.

Let Gf = (V, Ef) be the residual network of G induced by f.

Let h be a flow in Gf.

Define f + h to by (f + h )(u, v) = f(u, v) + h(u, v)

Lemma. f + h is a flow in G with value |f + h|= |f|+|h|

proof of Capacity constraint

(f + h )(u, v) = f(u, v) + h(u, v)

= -f(v, u) - h(v, u)

= -(f(v, u) + h(v, u))

= -(f + h )(v, u)

Augmenting Paths
Let G = (V, E) be a flow network and f be a flow in G.

Let Gf = (V, Ef) be the residual network of G induced by f.

An augmenting path p is a simple path from s to t in Gf

Residual capacity of p is the maximum amount of net flow that we can ship along the edges of p

cf(p) = min { cf(u, v) : (u, v) is on path p}

Residual Network	Flow in Residual Network

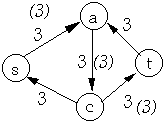Lemma. Let G = (V, E) be a flow network and f be a flow in G.

Let p be an augmenting path in Gf. Define hp : V * V -> R by:

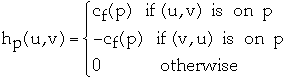
Then hp is a flow in Gf with value |hp| = cf(p).

Corollary

Let G = (V, E) be a flow network and f be a flow in G.

Let p be an augmenting path in Gf. Define hp as above.

Let k = f + hp. Then k is a flow in G with value

|k| = |f|+ | hp | > |f|

Ford-Fulkerson Method to find Maximum Flow
Let G = (V, E) be a flow network

initialize flow f to 0

while there exits an augmenting path p

do add hp to f

return f

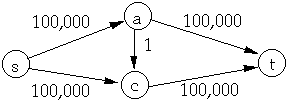
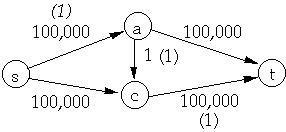
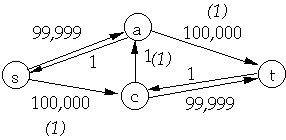
Let G = (V, E) be a flow network and f a flow in G
A cut (S, T) of G is a partition of V into S and T = V - S such that:

s [[propersubset]] S and t [[propersubset]] T

The net flow across the cut (S, T) is f(S, T)

The capacity of the cut (S, T) is c(S, T)

S = {s, c} T = { a, b, d, t}

f(S, T) = 3 + 6 - 4 + 8 = 13

c(S, T) = 16 + 10 + 14

Lemma
Let G = (V, E) be a flow network and f be a flow in G.

Let (S, T) be a cut of G. Then the net flow across (S, T) is

f(S, T) = |f|

proof:

f(S, T): = f(S, V - S)

= f(S, V - S)

= f(S, V) - f(S, S)

= f(S, V)

= f(s, V) + f(S - s, V)

= f(s, V)

= |f|

Corollary The value of any flow f in a flow network G is bounded from above by the capacity of any cut of G

The Max-flow min-cut theorem

Let f be a flow in G = (V, E) be a flow network with source s and sink t.

The following are equivalent:

1. f is a maximum flow in G

2. The residual network Gf contains no augmenting paths

3. |f| = c(S, T) for some cut (S, T) of G.

Ford-Fulkerson Algorithm to find Maximum Flow
Let G = (V, E) be a flow network

for each edge (u, v) [[propersubset]] E do

f[u, v] = 0
f[v, u] = 0

while there exits a path p from s to t in residual network Gf do

do cf(p) = min { cf(u, v) : (u, v) is on path p}
for each edge (u, v) in p do f[u, v] = f[u, v] + cf(p) f[u, v] = -f[v, u]

return f

How long does it take?

Edmonds-Karp Algorithm Find shortest path from s to t in Ford-Fulkerson

Let G = (V, E) be a flow network and f be a flow in G.

Let Gf = (V, Ef) be the residual network of G induced by f.

Let p be shortest path from s to t in Gf.

Define the flow

Let df(x, y) be the shortest-path distance from x to y in Gf

Let dh(x, y) be the shortest-path distance from x to y in Gh

Lemma 27.8 For all v [[propersubset]] V - {s, t} we have df(s, v) <= dh(s, v)
proof:

Assume that there exists v such that df(s, v) > dh(s, v)

Let v be the closes vertex to s for which this is true

Let sp be the shortest path from s to v in Gf

Let u be the vertex before v on sp and f[u, v] < c(u,v) then

df(s, v): = df(s, u) + 1

<= dh(s, u) + 1

= dh(s, v)

So we must have f[u, v] = c(u, v)

Thus (u, v) is not in Ef which means (v, u) is in Ef

So df(s, u)

= df(s, v) + 1

df(s, v)

= df(s, u) - 1

<= dh(s, u) - 1
= dh(s, v) - 2
< dh(s, v)

Theorem The Edmonds-Karp Algorithm will perform at most O(V*E) flow augmentations.
proof:

An edge (u, v) in a residual network Gf is critical on an augmenting path p if the residual capacity of p is the residual capacity of (u, v)

How many times can an edge be critical?


We have (draw picture)

df(s, v): = df(s, u) + 1

dh(s, u) = dh(s, v) + 1

So dh(s, u)

= dh(s, v) + 1

>= df(s, v) + 1
= df(s, u) + 2

Thus ( u, v) can be critical at most O(V) times

Since there are O(E) edges the total number of critical edges is O(E*V)

CS 660: Combinatorial Algorithms Graphs and Network Flows

Contents of Graphs and Network Flows Lecture

CS 660: Combinatorial Algorithms
Graphs and Network Flows