 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms
Intro To Binary Search Trees
[To Lecture Notes Index]
San Diego State University -- This page last updated Sept. 18, 1995

Contents of BST Lecture
- References
- Search Trees
- Tree Operations - Performance
- General Terms
Introduction to Algorithms by Cormen, Leiserson, Rivest. Chapter 13
Data Structures and Algorithms 1: Sorting and Searching, Mehlhorn, Kurt,
pages 174-177
Access (k, t): Return the item in tree t with key k; if no item in t has key k,
return null
Insert (j, t): Insert item j into t, not previously containing j
Delete (j, t): Delete item j from t
Minimum (t): Return the item in t with the smallest key
Maximum (t): Return the item in t with the largest key
Successor (k, t): Return the item in t with the smallest key larger than k
Predecessor (k, t): Return the item in t with the largest key smaller than k
Join (a, i, b): Return tree formed by combining tree a, item i, and tree b.
Assumes that every item in a has key less then key(i) and every item in b has
key larger than key(i)
Split (i, s): Split tree s, containing item i, into three trees: a, containing
all items with key less than key(i); single tree i; and b, containing all
items with key greater than key(i)
Types of Algorithms
Off-line
- Totally balanced BST
- Know all items in list
-
- Minimize worst case search
-
- Optimum BST
-
- Know all items and probability of access
-
- Minimize total search cost over all access
On-line
- Balanced BST (Weight, Height), Skip lists
-
- Add items as they show up
-
- Minimize worst case search
-
- Self-Adjusting BST
- Modify tree based on access pattern
Tree Operations on BST
Access, Minimum, Maximum, Successor, Predecessor, Insert
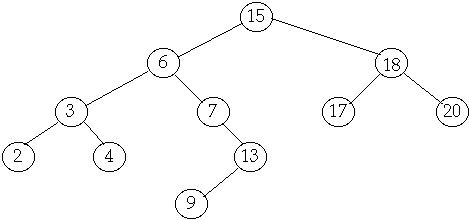
Tree Operations
Delete
Case
1 Delete leaf
Delete(20)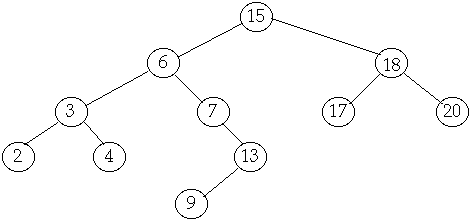
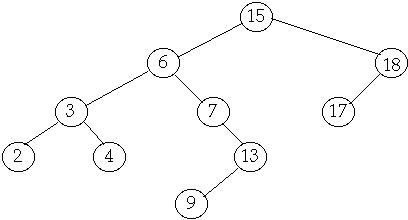 Tree Operations
Delete
Case
2 Delete node with one child
Delete(7)
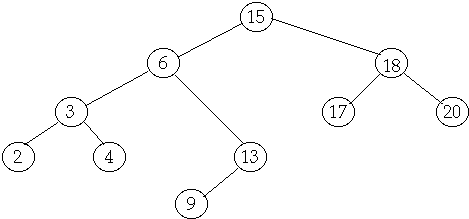
Tree Operations
Delete
Case
2 Delete node with one child
Delete(7)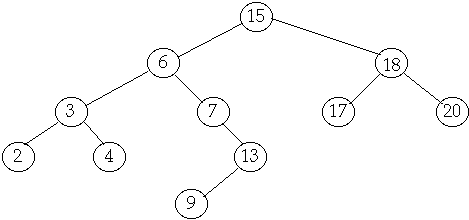
 Tree Operations
Delete
Case
3 Delete node with two children
Delete(6)
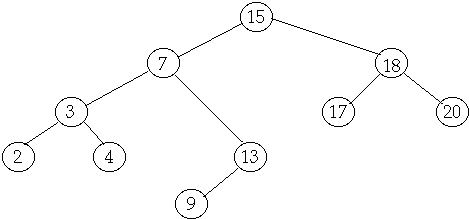
Tree Operations
Delete
Case
3 Delete node with two children
Delete(6)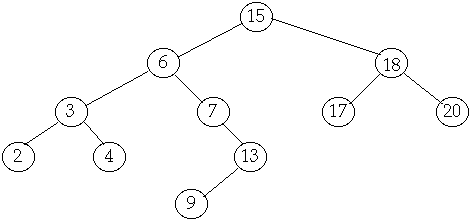
Theorem
- The operations Access, Minimum, Maximum, Successor, Predecessor, Insert,
and delete run in O(h) on a BST of height h
Randomly Built BST
Assume that we have n distinct keys in random order
Each n! permutations of the input keys is equally likely
Insert the keys in an empty tree, using random order
Theorem
- The average height of a randomly built BST on n distinct keys is O( lgn
)
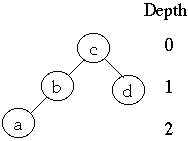
We have a list of n items: a1, a2, ..., an in BST
Probability of accessing item ak is P(ak) = Alphak
Let Betak be the probability of accessing a key that is between ak and
ak+1
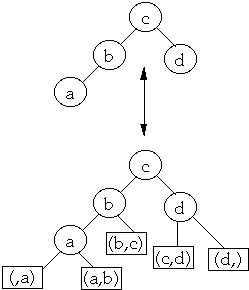
Let bk be the leaf between ak and ak+1
Betak is the probability of accessing leaf bk
Ordered by keys we have , b0< a1 <b1< a2 < ... < an < bn
(Beta0 ,Alpha1 ,Beta1 , Alpha2, Beta2,... ,
Alphan, Betan)1 is called the access distribution
Let
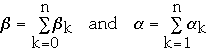
Weighted path length of a tree
Let D(ak) = depth of node ak
Define the weighted path length of tree T as:
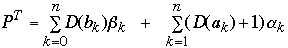
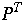 is the average number of comparisons in a search of T
is the average number of comparisons in a search of T
Entropy
Let (Gamma1 ,Gamma2,... , Gamman) be a discrete
probability distribution, i.e.
Gammak >= 0 and SigmaGammak =1
H(Gamma1 ,Gamma2,... , Gamman) =
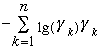
is the entropy of the distribution.
Use convention that 0*lg 0 = 0
Lower bound on weighted Path Length
We have a list of n items: a1, a2, ..., an in BST
Probability of accessing item ak is P(ak) = Alphak
Let bk be the leaf between ak and ak+1
Betak is the probability of accessing leaf bk
Let
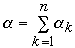
H = H(Beta0 ,Alpha1 ,Beta1 , Alpha2,
Beta2,... , Alphan, Betan)
P =
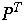
Theorem 5[2] For any BST we have:
- a)
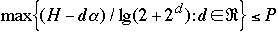
-
- b)
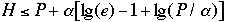
Self Organizing Linear List and BST
Is there the equivalent of Move-to-Front, Transpose and Optimal Static Ordering
in BST?
 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms