SDSU CS 660: Combinatorial Algorithms
Dynamic Lists

[To Lecture Notes Index]
San Diego State University -- This page last updated Sept. 5, 1995
----------

Contents of Dynamic Lists Lecture

  1. References
  2. Searching
  3. Self-Organizing Linear Search
    1. General Information and Restrictions
    2. Zipf's Law
    3. Lotka's Law
    4. 80% - 20% Rule
    5. Convergence to Steady State
    6. Known Algorithms and Analysis

References


Hester, James and Hirschberg, Daniel, "Self-Organizing Linear Search", Computing Surveys, 17(3):295-311, September 1985.

Searching


Search for x in a list of n data items
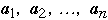
Standard Solution

* Sort the list of data items (or create a binary search tree)
Cost for general list is Theta(nlg(n))


* Now search for x
Average and worst case cost is Theta(lg(n))

Hidden Assumptions

* We will perform more than one search
Number of searches should be Omega(lg(n))


* All items in the list will be searched for with nearly the same frequency
Contrived Example

Assume we have a list of n items:

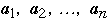
The a's are ordered by frequency of access

Probability of accessing item 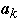: P( ) =

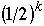
Probability of looking for an item not in the list is

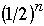
Average cost
U = set of all possible events
P(e) = probability of event e
C(e) = cost of event e

We have:

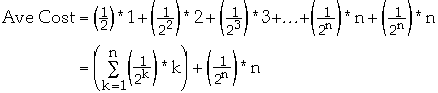
What is ?

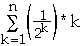We have:

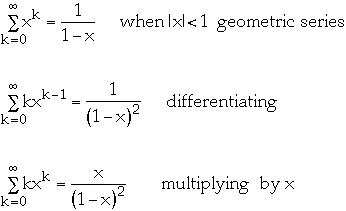
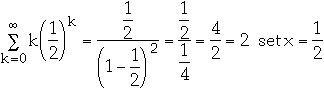
So

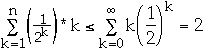
Thus Ave Cost =

Self-Organizing Linear Search

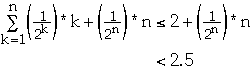
Why linear search?

* Simple to code
	location = -1
	for (K = 0; K < n; K++)
		if ( data[K].key == X)  {
	location = K;
	break;
	}

* Requires minimal space

Organizing the list

Assume we have a list of n items:

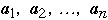
Probability of accessing item


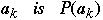
* Optimal Static Ordering


* Move-to-front


* Transpose
Optimal Static Ordering

Assume P(ak) is known for all k in advance

Order items in decreasing probability

Example: 2.0 average comparisons
Let P(a) = .2
P(b) = .4 P(c) = .3 P(d) = .1
Optimal static ordering
b, c, a, d

Move-to-front

Start with any initial ordering

When item is accessed move it to the front of the list

Example: 2.2 average comparisons
	a,	b,	c,	d	start order
	b,	a,	c,	d	accessed b	2 comparisons
	b,	a,	c,	d	accessed b	1
	a,	b,	c,	d	accessed a	2
	c,	a,	b,	d	accessed c	3
	a,	c,	b,	d	accessed a	2
	c,	a,	b,	d	accessed c	2
	c,	a,	b,	d	accessed c	1
	d,	c,	a,	b	accessed d	4
	b,	d,	c,	a	accessed b	4
	b,	d,	c,	a	accessed b	1
Transpose

Start with any initial ordering

When item is accessed move it forward one location

Example: 2.3 average comparisons
	a,	b,	c,	d	start order
	b,	a,	c,	d	accessed b	2 comparisons
	b,	a,	c,	d	accessed b	1
	a,	b,	c,	d	accessed a	2
	a,	c,	b,	d	accessed c	3
	a,	c,	b,	d	accessed a	1
	c,	a,	b,	d	accessed c	2
	c,	a,	b,	d	accessed c	1
	c,	a,	d,	b	accessed d	4
	c,	a,	b,	d	accessed b	4
	c,	b,	a,	d	accessed b	3

General Information and Restrictions


Permutation algorithms
Algorithm used to rearrange list after accessing a record


Restrictions
Only consider permutation algorithms that move accessed item forward in the list
Will not search for items not in the list
All items will be searched at least once
Time required by any execution of the permutation algorithm is never more than a constant times the time required for the search immediately before that execution.
Example
Given the list
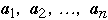
Accessing second item requires two comparisons so permutation algorithm can take c*2 time units
Accessing the last item requires two comparisons so permutation algorithm can take c*n time units
Measures of Performance

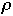the search sequence

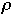[k] the item to be searched for on the k'th access

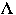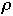(, k) be the state of the list after the first k accesses from [[rho]]

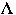(, k)r location in the list of item r after the first k accesses from [[rho]]

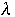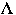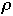= (, 0) the initial configuration of the list


Cost of a permutation 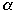for a given l and r is the average cost per access in terms of the number of probes required to find the accessed record and the work required to permute the records afterwards

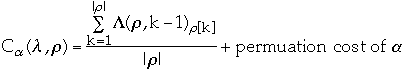
Asymptotic Cost
Average cost over all 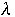and for a given
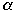
Usually restrict to make analysis possible

Zipf's Law


Zipf noticed that in English the frequency of word usage follows:

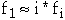
where fi denotes the frequency of the ith most frequent word


Zipfian Probability Distribution:

Assume we have a list of n items:

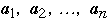
The a's are ordered by frequency of access

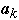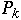Probability of accessing item is and

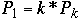
Then

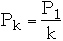
But 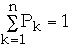so we have
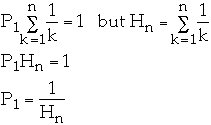
Zipfian Probability Distribution
Let 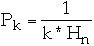for k = 1, 2, ..., n

where

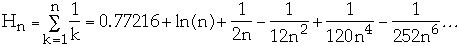
Pk 
n = 2

k	1	2

Pk	0.6667	0.3333



n = 3

k	1	2	3

Pk	0.5455	0.2727	0.1818



n = 4

k	1	2	3	4

Pk	0.48	0.24	0.16	0.12



n = 5

k	1	2	3	4	5

Pk	0.438	0.219	0.146	0.109	0.0876



n = 6

k	1	2	3	4	5	6

Pk	0.408	0.204	0.136	0.102	0.0816	.0680
How to Implement Zipf's Distribution

Let
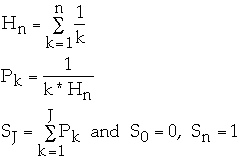
Method 1

If 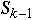<= rand() < 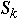then return k
Method 2

Lotka's Law


The number of papers in a given journal written by the same author follows an inverse square distribution.

Let n be the total number of authors who published at least one paper in a given journal.

The probability that a randomly chosen author contributed exactly k papers is given by:


n = 2
k	1	2
Pk	0.800	0.200

n =3
k	1	2	3
Pk	0.734	0.183	0.081

n =4
k	1	2	3	4
Pk	0.702	0.175	0.078	0.043

n =5
k	1	2	3	4	5
Pk	0.683	0.170	0.075	0.042	0.027

n =6
k	1	2	3	4	5	6
Pk	0.670	0.167	0.074	0.041	0.026	0.018

80% - 20% Rule


"80% of the transactions are on the most 20% of the records, and so on recursively"



When n = 5*L we have:
n = 2
k	1	2
Pk	0.908	0.100

n = 3
k	1	2	3
Pk	0.858	0.100	0.063

n = 4
k	1	2	3	4
Pk	0.825	0.100	0.063	0.047

n = 5
k	1	2	3	4	5
Pk	0.800	0.100	0.063	0.047	0.038
80% - 20% Rule


Knuth claims we can approximate this by:



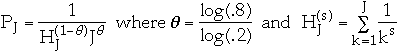
n = 2
k	1	2
Pk	0.644	0.355

n = 3
k	1	2	3
Pk	0.515	0.283	0.200

n = 4
k	1	2	3	4
Pk	0.446	0.245	0.173	0.135

n = 5
k	1	2	3	4	5
Pk	0.401	0.220	0.155	0.121	0.100

n = 6
k	1	2	3	4	5	6
Pk	0.369	0.203	0.143	0.111	0.092	0.078

Convergence to Steady State


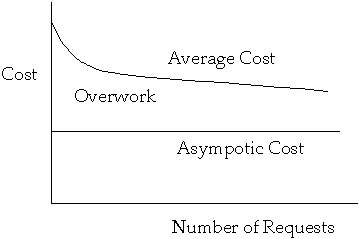
Steady State
Further permutations are not expected to change the expected search time significantly
Locality
Subsequences of [[rho]] may have relative frequencies of access that are drastically different from the overall relative frequencies
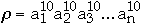
Total Number of Comparisons in searchWorst Case 
	n	Move-to-Front	BST
	7	112	170
	15	360	490
	31	1240	1290
	63	4536	3210
Measures of Convergence


Relative Measurements
Optimal Static Ordering - items are ordered by static probability of access and are not moved
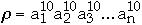
Total Number of Comparisons in searchWorst Case 
	n	Move-to-Front	OSO
	7	112	210
	15	360	1050
	31	1240	4650

Known Algorithms and Analysis


Move-to-front
Assume Zipf distribution

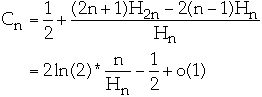
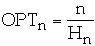
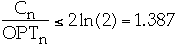
Transpose


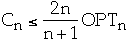
Count
approaches optimal static ordering
Comparisons between Algorithms

No Optimal Memoryless algorithm

Asymptotic Cost
Move-to-front asymptotic cost at most twice asymptotic cost of the optimal static ordering
Asymptotic cost of transpose is <= asymptotic cost of move-to-front
Count is asymptotically equal to optimal static ordering
Worst Case
Move-to-front and count at most twice the worst case of the optimal static ordering
Transpose can be far worse
Moving a record any fraction of the distance to the front of the list will be no more than a constant times the optimal off-line algorithm
The constant is inversely proportional to the fraction of the total distance moved