 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms
NP-Completeness
[To Lecture Notes Index]
San Diego State University -- This page last updated November 28, 1995

Contents of NP-Completeness Lecture
- Reference
- NP-Completeness
Computers and Intractability: A Guide to the Theory of NP-Completeness
by Garey and Johnson, Chapters 1, 2, 3
Intractable Problems
- Problems which can not be solved in polynomial time
Causes of Intractability
-
- Solution is too big
- Generate all permutations of N
- Problem is so hard it takes exponential time
Undecidable Problems
- Problems which can not be solved
-
- Halting Problem
- Input: a program and input for program
-
- Output: Will program halt on the input
Intractable and decidable Problems
- 1965 - First contrived example
-
- 1970's early - first natural example
P
All problems that can be solved in polynomial time
Decision Problems
Traveling Salesman Problem
- Instance:
- A finite set C = { c1, c2, ...., cm } of "cities"
- A integer valued distance function d(ci, ck) >= 0
- A bound B
-
- Question:
- Is there a tour of all the cities in C having total length no more than
B?
Nondeterministic Algorithm
Two stages
- Guessing Stage (the nondeterministic part)
-
- Guess solution to a decision problem
-
- Checking Stage (the deterministic part)
- Checks to determine if the guess is correct
A nondeterministic algorithm for a decision problem is said to "solve" the
problem in polynomial time if there is some guess, S, that leads the checking
stage to verify that S is correct in polynomial time
NP
Class of decision problems that can be solved in polynomial time by a
nondeterministic algorithm
Theorem. P is a subset of NP
Theorem. Let
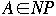 ,
then there exists a polynomial p such that A can be solved by a deterministic
algorithm having time complexity
,
then there exists a polynomial p such that A can be solved by a deterministic
algorithm having time complexity
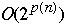
Polynomial Transformations
f is a polynomial transformation from decision problem A to decision problem B
if:
- f maps potential solutions of A to potential solutions of B
-
- f(x) can be computed in polynomial time
-
- x is a solution to A if and only if f(x) is a solution to B
If there exists a polynomial transformation from A to B we write

Lemma. Assume that
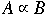 .
If B is in P the A is in P.
.
If B is in P the A is in P.
Lemma. If
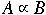 and
and
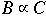 ,then
,then
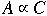
Example
Let G = (V, E)
Simple Circuit
- A sequence { v1, v2, ... , vk } of distinct vertices from V such that vn,
vn+1 is an edge and
-
- vk, v1 is an edge
-
- Hamiltonian Circuit
-
- Simple circuit that contains all vertices of G
Hamiltonian Circuit Problem (HC)
Instance: A graph G = (V, E)
Question: Does G contain a Hamiltonian circuit?
Traveling Salesman Problem (TS)
Instance:
- A finite set C = { c1, c2, ...., cm } of "cities"
- A integer valued distance function d(ci, ck) >= 0
- A bound B
Question:
- Is there a tour of all the cities in C having total length no more than
B?
Theorem
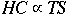
NP-Complete
Polynomial Equivalent
- A and B are polynomial equivalent if we have
 and
and
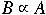
A decision problem, A, is NP-Complete if
-

-
- For all decision problems
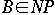 we have
we have
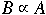
Cook's Theorem
Let U = { u1, u2, ..., um } be a set of Boolean variables
Literals over U. Let

- "u" and "not u" are literals over U
Clause over U is a set of literals
A clause is satisfied if an assignment of True, False to U makes one
member of the clause true
A collection, C, of clauses over U is satisfiable if and only if there exists
some truth assignment for U that simultaneously satisfies all the clauses in
C
Satisfiability
Instance:
- A set U of variable and a collection C of clauses over U
Question:
-
- Is C satisfiable
Cook's Theorem. Satisfiability is in NP-complete
 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms