 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms
Optimal BST
[To Lecture Notes Index]
San Diego State University -- This page last updated November 13, 1995

Contents of Optimal BST Lecture
- References
- Optimal BST
- Dynamic Programming
- Splay vs. OBST
- Nearly Optimal BST
- Optimal Alphabetic Tree1
- Algorithm for Nearly Optimal Lexicographic Tree6
Mehlhorn's Text, pages 177-187
Introaduction to Algorithms, Chapter16
Assume:
- We have a list of n items: a1, a2, ..., an
- Key(ak) = ak
- Probability of accessing item ak is known in advance and is P(ak)
- The list is ordered by keys, a1 <= a2 <= ... an
How to produce the BST that has the least search cost given the access
probability for each key?
Optimal BST
Greedy Algorithm fails
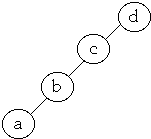
Example:
-
- list = a, b, c, d
- P(a) = .1, P(b) = .2, P(c) = .3, P(d) = .4
-
-
-
-
-
- Average Cost = 1*0.4 + 2*0.3 + 3*0.2 + 4*0.1 = 2.0
- Optimal BST
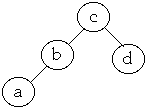
- Average Cost = 1*0.3 + 2*0.4 + 2*0.2 + 3*0.1 = 1.8
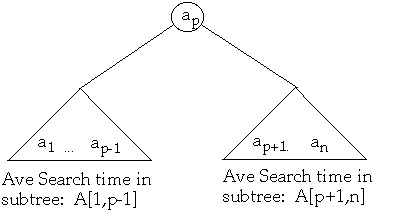
Finding the Optimal BST
Let A[j, k] = minimum average search time for a binary search tree with items
aj <= aj+1 <= ... ak
How to find A[1,n]?Set p = 1, 2, ..., n
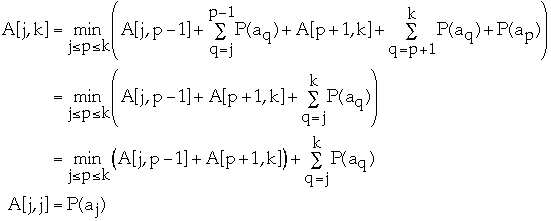
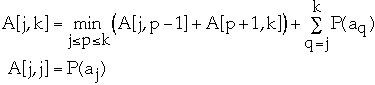
| j\k | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | P(a1) | | | | |
| 2 | 0 | 0 | P(a2) | | A[2,4] | |
| 3 | 0 | 0 | 0 | P(a3) | | |
| 4 | 0 | 0 | 0 | 0 | P(a4) | |
| 5 | 0 | 0 | 0 | 0 | 0 | P(a5) |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 |
Time Complexity for finding Optimal BST Theta(n3)
"Dynamic programming algorithm stores the results for small subproblems and
looks them up, rather than recomputing them, when it needs them later to solve
larger subproblems"
Baase
"Dynamic programming algorithm is very useful approach to many optimization
problems. ... Usually, we can find a tailor-made algorithm which is more
efficient than the straight-forward algorithm based on dynamic programming"
T. C. Hu
Steps in developing a dynamic programming algorithm
Characterize the structure of an optimal solution
Recursively define the value of an optimal solution
Compute the value of an optimal solution in a bottom-up fashion
Construct an optimal solution from computed information
Matrix-chain Multiplication
The Problem
Let A be a 10 * 100 matrix,
-
- B be a 100 * 5 matrix
- C be a 5 * 50 matrix
Then
- A * B is a 10 * 5 matrix
- B * C is a 100 * 50 matrix
Computing
-
- A * B takes 10 * 100 * 5 = 5,000 multiplications
-
- (A * B) * C takes 10 * 5 * 50 = 2,500 additional mult.
-
- So (A * B) * C requires total of 7,500 multiplications
Computing
-
- B * C takes 100 * 5 * 50 = 25,000 multiplications
-
- A * (B * C) takes 10 * 100 * 50 = 50,000 additional mult.
-
- So A * (B * C) requires total of 75,000 multiplications
But (A * B) * C = A * (B * C)
Matrix-chain Multiplication
The Problem
Given a chain <A1, A2, ..., An> matrices, where matrix Ak has dimension
pk-1 * pk fully parenthesize the product A1* A2*... *An, in a way that
minimizes the number of scalar multiplications
Characterize the structure of an optimal solution
Optimal solution is of the form:
- (A1* ... *Ak) * (Ak+1* ... *An)
not showing the parentheses in (A1* ... *Ak) or in (Ak+1* ... *An)
We must use the optimal parenthesization of A1* ... *Ak and the optimal
parenthesization of Ak+1* ... *An
Thus the optimal solution to an instance of the matrix-chain multiplication
problem contains within it optimal solutions to subproblem instances
That is it is recursive
Recursively define the value of an optimal solution
Recall matrix Ak has dimension pk-1 * pk for k = 1,..., n
Let m[k, w] be the minimum the number of scalar multiplications needed to
compute Ak* ... *Aw
If (Ak* ... *Az) * (Az+1* ... *Aw) is the optimal solution then
- m[k, w] = m[k, z] + m[z+1, w] + pk-1 * pz * pk
since (Ak* ... *Az) is a pk-1 * pz matrix
and (Az+1* ... *Aw) is a pz * pw matrix
But what is z?
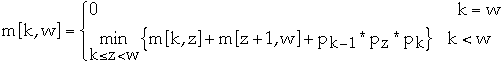
Compute the optimal solution in a bottom-up fashion
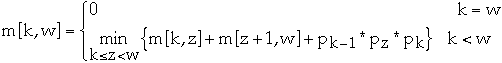
Example
Matrix dimension r pr
A1 10*20 0 10
A2 20*3 1 20
A3 3*5 2 3
A4 5*30 3 5
4 30
| 1 | 2 | 3 | 4 |
| 1 | 0 | 600 | 750 | 1950 |
| 2 | | 0 | 300 | 2250 |
| 3 | | | 0 | 450 |
| 4 | | | | 0 |
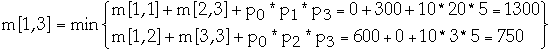
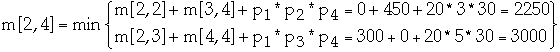
Construct an optimal solution
from computed information
Example
Matrix dimension r pr
A1 10*20 0 10
A2 20*3 1 20
A3 3*5 2 3
A4 5*30 3 5
4 30
| 1 | 2 | 3 | 4 |
| 1 | A1 | A1A2 | (A1A2)A3 | (A1A2)(A3A4) |
| 2 | | A2 | A2A3 | A2(A3A4) |
| 3 | | | A3 | A3A4 |
| 4 | | | | A4 |
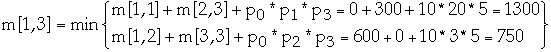
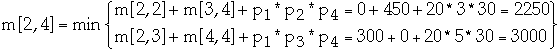
Time Complexity of building the OBST?
We have a list of n items: a1, a2, ..., an
Probability of accessing item ak is P(ak)
Let A[j, k] = minimum average search time for a binary search tree with items
aj <= aj+1 <= ... ak
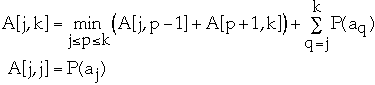
Let root[j,k] = p that gave the minimum value for A[j, k]
That is root[j,k] = root of OBST for items aj, a2, ..., ak
Let w[j,k] = P(aj) + P(aj+1) + ... + P(ak)
Constructing the OBST
for k = 1 to n do
- A[k, k] = P(ak)
- A[k, k-1] = 0
- root[k,k] = k
- w[k, k] = P(ak)
end
A[n+1, n] = 0
for diagonal = 1 to n -1 do
- for j = 1 to n - diagonal do
- k = j + diagonal
-
- w[j, k] = w[j, k - 1] + P(ak)
-
- let p, j <= p <= k, be the value minimizes:
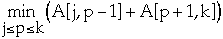
-
- root[j,k] = p
-
- A[j, k] = A[j, p-1] + A[p+1, k] + w[j, k]
- end for
end for
Example 1
k 1 2 3 4 5 6
ak a b c d e f
P(ak)'s = 0.4 0.05 0.15 0.05 0.1 0.25
root
1 1 1 1 1 3
0 2 3 3 3 5
0 0 3 3 3 5
0 0 0 4 5 6
0 0 0 0 5 6
0 0 0 0 0 6
A
0 0.4 0.5 0.85 1 1.35 2.1
0 0 0.05 0.25 0.35 0.6 1.2
0 0 0 0.15 0.25 0.5 1.05
0 0 0 0 0.05 0.2 0.6
0 0 0 0 0 0.1 0.45
0 0 0 0 0 0 0.25
0 0 0 0 0 0 0

Example 2
P(ak)'s = (0.15 0.025 .05 .025 .05 .125 .025 .075 0.075 .05 .15 .075 .05 .025
.05)
Root
1 1 1 1 1 3 3 6 6 6 6 6 6 6 6
0 2 3 3 3 5 6 6 6 6 6 9 9 9 11
0 0 3 3 3 5 6 6 6 6 9 9 9 9 11
0 0 0 4 5 6 6 6 6 6 9 9 9 9 11
0 0 0 0 5 6 6 6 6 8 9 9 9 11 11
0 0 0 0 0 6 6 6 8 8 9 9 11 11 11
0 0 0 0 0 0 7 8 8 9 9 11 11 11 11
0 0 0 0 0 0 0 8 8 9 9 11 11 11 11
0 0 0 0 0 0 0 0 9 9 11 11 11 11 11
0 0 0 0 0 0 0 0 0 10 11 11 11 11 11
0 0 0 0 0 0 0 0 0 0 11 11 11 11 11
0 0 0 0 0 0 0 0 0 0 0 12 12 12 13
0 0 0 0 0 0 0 0 0 0 0 0 13 13 13
0 0 0 0 0 0 0 0 0 0 0 0 0 14 15
0 0 0 0 0 0 0 0 0 0 0 0 0 0 15
A[1,15] = 2.925
Modified Algorithm
for diagonal = 1 to n -1 do
- for j = 1 to n - diagonal do
- k = j + diagonal
- w[j, k] = w[j, k - 1] + P(ak)
-
- let p, root[j,k-1] <= p <= root[j+1,k], be the value
minimizes:
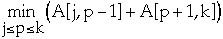
-
- root[j,k] = p
-
- A[j, k] = A[j, p-1] + A[p+1, k] + w[j, k]
- end for
end for
Time Complexity
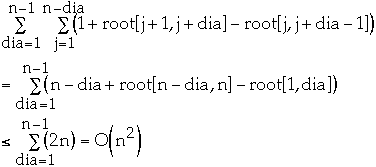
General Theorem
Let H(i, j) be a real number for 1 <= i < j <= n
Let c(i, j) be defined by:
- c(i, i) = 0
-
- c(i, j) = H(i, j) +
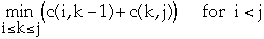
Let K(i, j) = largest k, i <= k <=j, that minimizes c(i, k-1) + c(k,
j)
H(i, j) is monotone with respect to set inclusion of intervals if
- H(j, k) <= H(x, y) if j <= x < y <= k
H(i, j) satisfies the quadrangle inequality (QI) if
- H(j, k) + H(x, y) <= H(x, k) + H(j, y) if j <= x < k <=
y
Theorem. If H(i, j) satisfies QI and is monotone then c(i, j) can be
computed in time O(n2)
Lemma. If H(i, j) satisfies QI and is monotone then c(i, j) satisfies
QI
Lemma. If c(i, j) satisfies QI then we have
-
- K(i, j) <= K(i, j+ 1) <= K(i+1, j+1)
Recall in OBST we have:
- We have a list of n items: a1, a2, ..., an and leaves b0, b1, ..., bn
-
- Probability of accessing item ak is P(ak) = Alphak
-
- Let Betak be the probability of accessing a key that is between ak
and ak+1, that is leaf bk
In splay tree we have Betak = 0, and Alphak = q(i)/m
Theorem 9: Let Popt be the be the weighted path length of optimum BST. We
have:
-

- where H = H(Beta0 ,Alpha1 ,Beta1 , Alpha2,
Beta2,... , Alphan, Betan) is entropy
Thus we have:
-
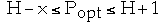 for some x
for some x
Since Popt is the average path length the total time spent to perform m
accesses is m*Popt.
Now:
-
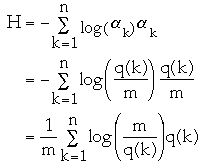
So m*H =
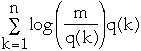
Thus: m*Popt <= m*H + 1 =
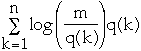 + m
+ m
We have a list of n items: a1, a2, ..., an
Probability of accessing item ak is P(ak)
k 1 2 3 4 5 6
ak a b c d e f
P(ak)'s = 0.4 0.05 0.15 0.05 0.1 0.25
Method 1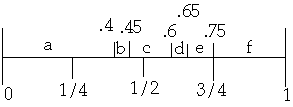
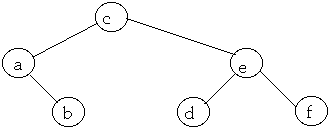
Average Access Cost = 2.2
Nearly Optimal BST
k
1 2 3 4 5 6
ak a b c d e f
P(ak)'s = 0.4 0.05 0.15 0.05 0.1 0.25
Method 2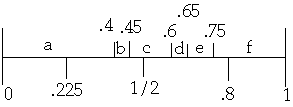
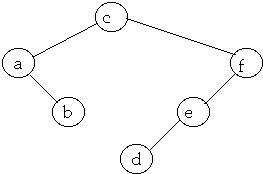
Average Access Cost = 2.1
An alphabetic tree is a binary search tree in which all data is in the leaves.
Internal nodes are used in search for the data

Let V1, V2,... Vn be the order of the leaves
Let wk be the weight, or frequency of access, of leaf Vk
Combining Vk and Vp, denote their parent node by Vkp and it weight wkp = wk+
wp
All leaves are square nodes, all parents are round nodes
Optimal Alphabetic Tree: Definitions
Two nodes are a compatible pair if they are adjacent or if all nodes between
them are round nodes
The weight of a pair is the weight of the parent of the two nodes
A pair with minimum weight over all pairs is a minimum pair
Minimum compatible pair is the compatible pair with the least weight over all
compatible pairs
- Ties are broken by taking the pair with the left most left node
-
- If two compatible pairs have the same left node and the same weight, then
pick the pair with the leftmost right node
Hu-Tucker Algorithm
1. Construction
- Find the minimum compatible pair
- Replace the left node of the pair by the pair's parent
- Remove right node of the pair
-
- Repeat n-1 times
-
- Call the resultant tree T'
2. Level Assignment
- Determine the level number Lk of every leaf Vk in T'
3. Reconstruction
- We have the level numbers L1, L2,... Ln of all leaves
-
- Find the leftmost maximum level number, say Lk = q
-
- Then Lk+1 = q
-
- Replace Lk and Lk+1 with a parent node with level q - 1
-
- Repeat n - 1 times
Theorem. The Hu-Tucker algorithm can be implemented to produce the optimal
alphabetic tree with N leaves in O(Nlg(N)) time and O(N) space
How Well Does OBST and NOBST Perform?
We have a list of n items: a1, a2, ..., an and leaves b0, b1, ..., bn
Probability of accessing item ak is known in advance and is P(ak) =
Alphak
Let Betak be the probability of accessing a key that is between ak and
ak+1, that is leaf bk
The list is ordered by keys, b0< a1 <b1< a2 < ... < an <
bn
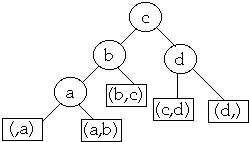
(Beta0 ,Alpha1 ,Beta1 , Alpha2, Beta2,... ,
Alphan, Betan) is the access distribution
Let
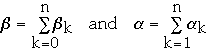
Let L(ak) be the level of the node ak
Let
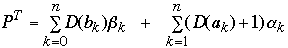
P is the weighted path length of a tree
Let (Gamma1 ,Gamma2,... , Gamman) be a discrete
probability distribution, i.e.
Gammak >= 0 and SigmaGammak =1
H(Gamma1 ,Gamma2,... , Gamman) =
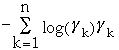
is the entropy of the distribution. ( 0*log 0 = 0)
Let TBB be the tree resulting from the nearly optimal BST algorithm 1
Theorem 7[2]: Let L(ak) be the depth of node ak
and let L(bk) be the depth of leaf bk in tree TBB Then
-
- bk <= floor (log 1/bk) + 2
- ak <= floor (log 1/ak)
Theorem 8[3]: Let PBB be the weighted path
length of the tree TBB. Then
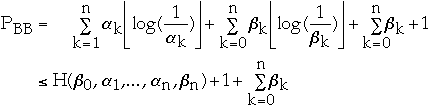
Theorem 9[4]: Let PBB be the weighted path
length of tree TBB. Let Popt be the be the weighted path length of optimum
BST. We have:
-
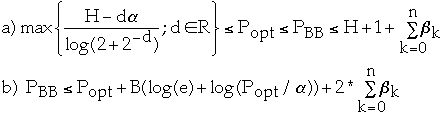
- where H = H(Beta0 ,Alpha1 ,Beta1 , Alpha2,
Beta2,... , Alphan, Betan) and
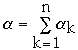
This gives us
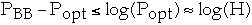 Example.
Example.
In English, the probability of occurrence of the i-th most frequent word is
approximately[5]
-

This yields
H(Alpha1 ,Alpha2, ... ) = 10.2
The weighted path length of an optimum binary search tree for all
English words is no larger than 11.2.
Nearly Optimal BST
We have a list of n items: a1, a2, ..., an
Probability of accessing item ak is P(ak)
k 1 2 3 4 5 6
ak a b c d e f
P(ak)'s = 0.4 0.05 0.15 0.05 0.1 0.25
Method 1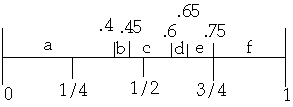
Problem:
k 1 2 3
ak a b c
P(ak)'s = 0.45 0.1 0.45
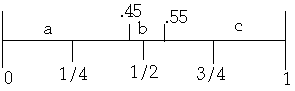
Given the ordered set {a} of names, such that a1 <= a2 <= ... an , and
two parameters, F and N0
(1) If N <= N0 , use dynamic programming.
(2) If N> N0, let W[k, l] be the weight of the subtree with frequencies
- Betak ,Alphak+1 ,Betak+1 , ... , Alphal,
Betal
-
- F a parameter and AC the centroid.
- Form the ordered set of names {AF} = {AL} union AC,
- where the members of the set {AL} satisfy
|W[O,L-1] - W[L,N]| < W[O,N]/F, 1 <= F <= W[O,N]
(3) Find an index, max, such that Alphamax = maximum Alphai,
where ai is in {AF}.
(4) If in the set {AF} there is at least one name preceding or equal to AC with
associated frequency Alphamax, let p be the index such that ap with
Alphap = Alphamax, is lexicographically closest to AC.
- If there is no such p, let {AQ} be the null set and go to Step 6.
(5) If ap is the first member of {AF} and Alphap-1 > Alphap,
form the set {AQ} = {ap-1 , ap-2, ., au}, where Alphap-j-1 >
Alphap-j , j = 0, ... ,p-u-1 and Alphau-1 <= Alphau or
u-p = floor(lg N);
- if ap is not the first member of {AF}, let {AQ} be the null set.
(6) If in the set {AF} there is at least one name following or equal to AC with
associated frequency Alphamax let r be the index such that ar with
Alphar = Alphamax is lexicographically closest to AC;
- if there is no such r, let {AS} be the null set and go to Step 8.
(7) If ar is the last member of {AF} and Alphar<Alphar+1, form
the set {AS}= {ar+1, ar+2,...,av}, where Alphar+j<Alphar+j+1,
j=0, 1, ... ,v-r-1, and Alphav>=Alphav+1or v-r = floor(lg N).
- If ar is not the last member of {AF}, let {AS} be the null set.
(8) Find an index, root, such that Alpharoot = maximum Alphai,
where ai is in {AQ} union {AF}union{AS} and |W[O,root-1] - W[root,N]|
is minimized; choose aroot as the root of the tree.
(9) Go to Step 1 and repeat the algorithm for the subtrees a1, a2, ... aroot-1
and aroot+1, ... aN, where N is root-I and N-root for the two cases.
Picking N0 and F
if Beta/Alpha is small (<= 3) than use N0= 15
if Beta/Alpha is large (> 3) than use N0= 25 or 30
if Beta/Alpha is large (> 2) than use F = 6
if Beta/Alpha ~ 1 than use F = 4
if Beta/Alpha < 1 than use F = 4
The tree takes O(Nlog(N)) to construct
Average search time for NOBST is within 2% of the average search time of the
OBST
Average Search Length
N0= 15, F = 5
| N | Alpha freq | Beta freq | OBST | NOBST |
| 5 | 19,846 | 982,497 | 3.4114 | 3.4114 |
| 15 | 42,653 | 959,690 | 4.2864 | 4.2864 |
| 25 | 60,087 | 942,256 | 5.0638 | 5.1033 |
| 50 | 92,117 | 910,226 | 6.0483 | 6.1461 |
| 100 | 138,975 | 863,368 | 7.0007 | 7.0437 |
| 150 | 173,157 | 829,186 | 7.4885 | 7.5503 |
| 200 | 200,412 | 801,931 | | 7.8795 |
| 500 | 305,266 | 697,077 | | 8.9606 |
| 1000 | 401,288 | 601,055 | | 9.6490 |
| 3000 | 561,956 | 440,387 | | 10.6220 |
| 6000 | 655,538 | 346,805 | | 11.1177 |
| 12000 | 740,022 | 262,321 | | 11.1592 |
| |
 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms