CS 660: Combinatorial Algorithms
Tree Performance
[To Lecture Notes Index]
San Diego State University -- This page last updated October 31, 1995
Contents of Tree Performance Lecture
- References
- Performance
- Baer and Schwab Tests
- Implementation-Independent Measures
- Time Results
Handbook of Algorithms and Data Structures, by G. H. Gonnet
A Comparison of Tree-Balancing Algorithms, Baer and Schwab, CACM, V 20, Num 5,
May 1977, pp 322-330
n = number of nodes in the tree
C(n) = average number of comparisons to find a key
E[ h(n) ] = expected height of tree
R(n) = average number of rotations per insertion/deletion
Simulation Results Binary Search TreesRandom Input
| n | C(n) | E[ h(n) ] |
| 5 | 2.48 | 3.8 |
| 10 | 3.444 | 5.6 |
| 50 | 6.178 | 10.810 |
| 100 | 7.479 | 13.286 |
| 500 | 10.613 | 19.336 |
| 1000 | 11.986 | 22.036 |
| 5000 | 15.193 | 28.428 |
| 10000 | 16.577 | 31.222 |
Simulation Results AVL
| n | C(n) | E[ h(n) ] | R(n) |
| 5 | 2.2 | 3.0 | 0.213 |
| 10 | 2.907 | 4.0 | 0.318 |
| 50 | 4.930 | 6.947 | 0.427 |
| 100 | 5.889 | 7.999 | 0.444 |
| 500 | 8.192 | 10.923 | 0.461 |
| 1000 | 9.202 | 11.998 | 0.463 |
| 5000 | 11.555 | 14.936 | 0.465 |
| 10000 | 12.568 | 15.996 | 0.465 |
Simulation Results BB[ 1 -
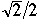] trees
| n | C(n) | E[ h(n) ] | R(n) |
| 5 | 2.2 | 3.0 | 0.213 |
| 10 | 2.9 | 4.0 | 0.326 |
| 50 | 4.944 | 7.026 | 0.409 |
| 100 | 5.908 | 8.208 | 0.422 |
| 500 | 8.231 | 11.261 | 0.432 |
| 1000 | 9.245 | 12.588 | 0.433 |
| 5000 | 11.618 | 15.653 | 0.435 |
| 10000 | 12.650 | 17.000 | 0.434 |
Algorithms
AVL
BB[ 1 -
]
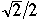COM - complete restructuring of tree
Input
N = 1000
R = random input
W = worst case
- 1, 1000, 2, 999, 3, ...
Hardware
CDC 6400
Random input
| Tree | Max Level | Ave path | Av insert. | Rotations |
| | | length | path | |
| Random | 22.6 | 12.14 | 12.14 | 0 |
| AVL | 12. | 9.20 | 9.73 | 461 |
| BB | 12.6 | 9.26 | 9.70 | 426 |
| COM | 11.8 | 9.06 | 9.68 | 12.8 |
Worst Case input
| Tree | Max Level | Ave path | Av insert. | Rotations |
| | | length | path | |
| Random | 1000 | 500.5 | 500.5 | 0 |
| AVL | 12 | 9.27 | 11.51 | 988 |
| BB | 13 | 9.36 | 12.32 | 1041 |
| COM | 30 | 9.20 | 18.11 | 74 |
| Tree | Random | Worst Case |
Random
| 0.58 | >10 |
AVL
| 0.96 | 1.06 |
BB 1 -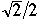 
| 2.20 | 2.84 |
BB .25
| 2.36 | 3.68 |
BB .15
| 2.32 | 5.34 |
COM
| 0.93 | 3.61 |
Questions Addressed
Assuming that most trees are random, what is the ratio of the number of
insertions to the number of subsequent queries which make a balancing
worthwhile?
AVL Tree 3 queries per insertion
BB Tree 10 queries per insertion
What is the best algorithm?
AVL