 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms
SkipLists
[To Lecture Notes Index]
San Diego State University -- This page last updated October 10, 1995

Contents of SkipLists Lecture
- Skip Lists: BST Las Vegas Style
- Deleting a Node
- Adding a Node
- Timing results
Level K node - a node with k forward pointers
In above example we have 1/2k nodes at level k
Need lg(n) levels to act like BST
Let p = be the fraction of the nodes with level j pointers that also have level
j + 1 pointers
p = 1/3
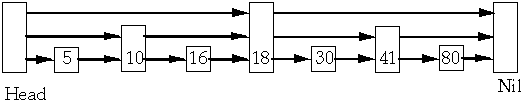
1. Find the node
2. Remove it
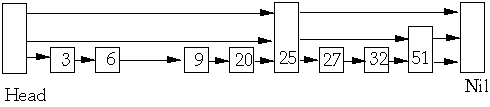
Delete 7
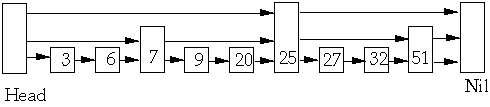
Resultant List
For a skip list need to select a value for p
1. Select the level of the node
2. Add the node in the proper location
Selecting the level - Theory
Select level k with probability pk
-
- newLevel = 1;
- while random() < p do
-
- newLevel = newLevel + 1
Selecting the level - Practice
Let N be an upper bound on the number of nodes in the list
Let MaxLevel =
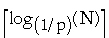
Let CurrentMax be the highest level currently in the list
- newLevel = 1;
- while random() < p do
-
- newLevel = newLevel + 1
-
- return min(newLevel, CurrentMax + 1, MaxLevel)
Adding Example, p = 1/3
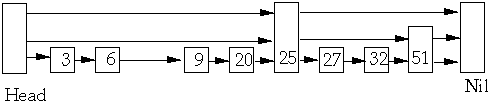
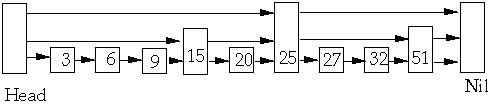
Add 15
random number generator returns .04 and .672
So level is 2
Resultant List
List contains 216 elements
Time does not include memory management time
Paper does not include information about access distribution
Time in msec
| Algorithm | Search | Insertion | Deletion |
| Skip List | 0.051 | 0.065 | 0.059 |
| non-recursive AVL | 0.046 | 0.10 | 0.085 |
| recursive 2-3 tree | 0.054 | 0.21 | 0.21 |
| top-down-splay | 0.15 | 0.16 | 0.18 |
| bottom-up splay | 0.49 | 0.51 | 0.53 |
Performance relative to Skip List
| Algorithm | Search | Insertion | Deletion |
| Skip List | 1.0 | 1.0 | 1.0 |
| non-recursive AVL | 0.91 | 1.55 | 1.46 |
| recursive 2-3 tree | 1.05 | 3.2 | 3.65 |
| top-down-splay | 3.0 | 2.5 | 3.1 |
| bottom-up splay | 9.6 | 7.8 | 9.0 |
 CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms CS 660: Combinatorial Algorithms
CS 660: Combinatorial Algorithms