 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
Fall Semester, 1996
NP Completeness
[To Lecture Notes Index]
San Diego State University -- This page last updated Dec 5, 1996

Contents of NP Completeness
- Reference
- NP Completeness
Introduction to Algorithms, by Cormen, Leiserson, Rivest, Chapter 36
Abstract problem Q
- Q is a binary relation on set of problem instances I and a set of problem
solutions S
-
-
Example - Shortest Path
- Find the shortest path in a graph between two vertices.
- I = { (G, s, e) | G = (V, E) is unweighted undirected graph, s
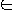 V
is the start vertex, e
V
is the start vertex, e
 V
is the end vertex }
V
is the end vertex }
- S = { (G, p) | G = (V, E), p is a path in G }
- Let a =( G, s, e )
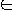 I then
I then
Q(a) = { (G, p) |p is the shortest path between s and e in G }
-
-
-
- Usually use Shortest Path instead of Q
Decision Problems - Problems with yes/no answers
- Given a graph G = (V, E) and two vertices s, e
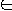 V does there exist a path in G between s and e whose length is at most k?
V does there exist a path in G between s and e whose length is at most k?
-
- I = { (G, s, e, k) | G = (V, E) is unweighted undirected graph, s
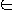 V is the start vertex, e
V is the start vertex, e
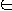 V is the end vertex, k upper bound on shortest path }
V is the end vertex, k upper bound on shortest path }
- S = { 0, 1 }
- Let a = ( G, s, e, k )
 I then
I then
- Path(a) = 1 if shortest path from s to e has length <= k
-
- Path(a) = 0 if shortest path from s to e has length > k
-
-
-
Decision problems simplify theory
Most problems can be restated as a decision problem
Concrete Problem is a problem whose instance is the set of binary
strings
Example:
- Let x be an integer, is x even?
-
- Let I = { binary strings}, S = { 0, 1 }
-
- Let x
 I then we have
I then we have
-
- Even(x) = 1
- if x1 = 1
-
- Even(x) = 0
- if x0 = 1
An algorithm solves a concrete problem in time O(T(n)) if
- given a
 I with n = |a| the algorithm finds the solution in at most O( T(n) )
time
I with n = |a| the algorithm finds the solution in at most O( T(n) )
time
Polynomial-time solvable
- A concrete problem is polynomial-time solvable if there exits an algorithm
to solve it in time O(nk) for some constant k
Complexity class P = { concrete problem that are polynomial-time
solvable }
Encodings
- An encoding "e" is a mapping from a set S to binary strings
Use encodings to map abstract problems to concrete problems
Example - Shortest Path
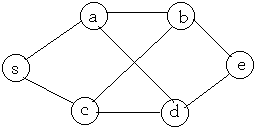
s a b c d e
s 0 1 0 1 0 0
a 1 0 1 0 1 0
b 0 1 0 1 0 1
c 1 0 1 1 0 0
d 0 1 0 1 0 1
e 0 0 1 0 1 0
010100101010010101101100010101001010
Encodings change the time complexity
Example Is K a prime number?
- Algorithm
- divide K by all integers 2, 3, 4, ..., K -1
-
- If any integer divides K it is not prime
-
- Worst case requires K -2 divisions (Use K for simplicity)
-
-
-
-
- Embedding 1 K -> binary representation of K
- Input length is n = lg(K)
-
- Time Complexity T(n) = K = 2n
-
-
-
- Embedding 2 Place the J'th bit of K in location 2J, fill
rest of locations with 0.
- Input length is n = K
-
- Time Complexity T(n) = n
f : {0, 1}* -> {0, 1}* is polynomial-time
computable if there exists a polynomial-time algorithm A that, given any
input x
 {0, 1}*, produces as output f(x)
{0, 1}*, produces as output f(x)
Given set of problem instances I, encodings e1 and e2
are polynomially related if there exists polynomial-time computable
functions f1 and f2 such that
- a
 I -> f1( e1( a ) ) = e2( a ) and
f2( e2( a ) ) = e1( a )
I -> f1( e1( a ) ) = e2( a ) and
f2( e2( a ) ) = e1( a )
Lemma
- Let Q be an abstract decision problem on an instance set I, and let
e1 and e2 be encodings polynomially related encodings on
I. Then
-
- e1( Q )
 P if and only if e2( Q )
P if and only if e2( Q )
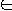 P
P
The Final Step - Formal-language
Alphabet
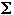 a finite set of symbols
a finite set of symbols
Language L over
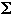
- any set of strings made up of symbols from
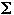
Empty string denoted by
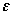
Empty language by
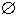
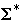 language of all strings over
language of all strings over
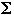
Complement of L
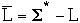
Concatenation of two languages L1 and L2 is the
language:
- L = { xy : x
 L1
and y
L1
and y
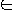 L2 }
L2 }
Closure or Kleene Star of L is
-
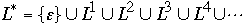
-
Decision Problems as a language
- Let
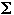 = {0, 1} then set of binary strings =
= {0, 1} then set of binary strings =
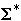
-
- Let Q be a decision problem
-
- L = {x
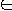
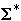 : Q(x) = 1 }
: Q(x) = 1 }
Algorithm A accepts a string x
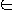 {
0, 1 }* if A(x) = 1
{
0, 1 }* if A(x) = 1
Algorithm A rejects a string x
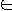 {
0, 1 }* if A(x) = 0
{
0, 1 }* if A(x) = 0
The language accepted by algorithm A is
- L = { x
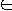 {
0, 1 }* : A(x) = 1}
{
0, 1 }* : A(x) = 1}
A language L is decided by algorithm A if every binary string is either
accepted or rejected by algorithm A
A language L is accepted in polynomial time by algorithm A if for any string of
length n in L is accepted by A in time O(nk)
A language L is decided in polynomial time by algorithm A if for any string of
length n in { 0, 1 }* is decided by A in time O(nk)
We can redefine P as:
P = {
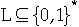 : there exists an algorithm A that decides L in polynomial time }
: there exists an algorithm A that decides L in polynomial time }
Theorem
- P = { L : L is accepted by a polynomial-time algorithm }
Polynomial-time Verification
Hamiltonian cycle of an undirected graph G= (V, E) is a simple cycle
that contains each vertex in V
A hamiltonian graph is a graph that has a hamiltonian cycle.
Let m = |V|, it takes m! operations to determine if G= (V, E) is a hamiltonian
graph
If Mary claims a graph is hamiltonian graph and provides a the vertices in
order on the hamiltonian cycle then we can verify his claim in polynomial
time
The potential cycle is called the certificate.
A verification algorithm is a two-argument algorithm A
One argument is an ordinary input string x, the other is the
certificate a binary string y.
"A" verifies input x if there exists a certificate such that
A(x, y) = 1
The language verified by A is:
L = { x
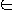 {
0, 1 }* : there exists y
{
0, 1 }* : there exists y
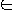 {
0, 1 }* such that A(x, y) = 1}
{
0, 1 }* such that A(x, y) = 1}
Complexity Class NP
Complexity class NP is the class of languages that can be verified by a
polynomial-time algorithm
Theorem
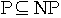
proof:
If L
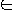 P
then L is accepted in polynomial time by algorithm B
P
then L is accepted in polynomial time by algorithm B
- That is for any x
 L
we can compute B(x) in polynomial time and B(x) = 1
L
we can compute B(x) in polynomial time and B(x) = 1
-
- Now let A( x ,y ) = B( x )
-
- Then A( x, y ) verifies x in polynomial time
Language L1 is polynomial-time reducible to language
L2 if there exists a polynomial-time computable function
- f : { 0, 1 }* -> { 0, 1 }*
such that for all x
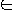 {
0, 1 }* we have:
{
0, 1 }* we have:
- x
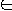 L1
if and only if f( x )
L1
if and only if f( x )
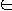 L2
L2
We write L1 <=p L2
Lemma 36.3 Assume that L1 <=p L2, then L2
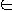 P
implies L1
P
implies L1
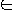 P
P
A language
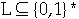 is NP-complete if
is NP-complete if
1. L
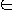 NP
NP
2. L1 <=p L for all L1
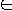 NP
NP
Theorem 36.4
- a. If any NP-complete problem is polynomial solvable then
-
- P = NP.
- b. If any NP-complete problem is not polynomial solvable then all
NP-complete problems are not polynomial solvable
 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms V
is the start vertex, e
V
is the start vertex, e
 V
is the end vertex }
V
is the end vertex }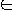 I then
I then
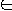 V does there exist a path in G between s and e whose length is at most k?
V does there exist a path in G between s and e whose length is at most k?
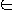 V is the start vertex, e
V is the start vertex, e
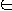 V is the end vertex, k upper bound on shortest path }
V is the end vertex, k upper bound on shortest path }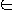 I then
I then
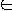 I then we have
I then we have
 I with n = |a| the algorithm finds the solution in at most O( T(n) )
time
I with n = |a| the algorithm finds the solution in at most O( T(n) )
time

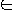 {0, 1}*, produces as output f(x)
{0, 1}*, produces as output f(x)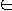 I -> f1( e1( a ) ) = e2( a ) and
f2( e2( a ) ) = e1( a )
I -> f1( e1( a ) ) = e2( a ) and
f2( e2( a ) ) = e1( a )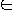 P if and only if e2( Q )
P if and only if e2( Q )
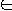 P
P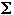 a finite set of symbols
a finite set of symbols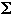
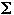
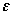
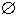
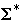 language of all strings over
language of all strings over
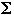
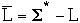
 L1
and y
L1
and y
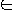 L2 }
L2 }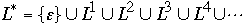
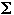 = {0, 1} then set of binary strings =
= {0, 1} then set of binary strings =
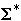
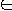
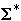 : Q(x) = 1 }
: Q(x) = 1 }
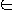 {
0, 1 }* if A(x) = 1
{
0, 1 }* if A(x) = 1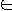 {
0, 1 }* if A(x) = 0
{
0, 1 }* if A(x) = 0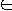 {
0, 1 }* : A(x) = 1}
{
0, 1 }* : A(x) = 1}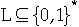 : there exists an algorithm A that decides L in polynomial time }
: there exists an algorithm A that decides L in polynomial time }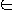 {
0, 1 }* : there exists y
{
0, 1 }* : there exists y
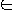 {
0, 1 }* such that A(x, y) = 1}
{
0, 1 }* such that A(x, y) = 1}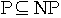
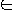 P
then L is accepted in polynomial time by algorithm B
P
then L is accepted in polynomial time by algorithm B L
we can compute B(x) in polynomial time and B(x) = 1
L
we can compute B(x) in polynomial time and B(x) = 1
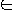 {
0, 1 }* we have:
{
0, 1 }* we have: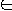 L1
if and only if f( x )
L1
if and only if f( x )
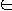 L2
L2
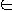 P
implies L1
P
implies L1
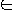 P
P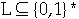 is NP-complete if
is NP-complete if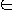 NP
NP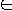 NP
NP