 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
Fall Semester, 1996
B-Trees, (a,b)-Trees
[To Lecture Notes Index]
San Diego State University -- This page last updated Oct 10, 1996

Contents of B-Trees, (a,b)-Trees
- References
- B-Trees of degree t
- Insertion in a B-Tree
- Deletion in a B-Tree
- B-Trees and Red-Black Trees
- ( a, b )-Trees
- Insertion
- Deletion
- Amorized Cost
- A-Sort
Introduction to Algorithms, Chapter 19
Data Structures and Algorithms 1: Sorting and Searching, Mehlhorn,
sections 5.2, 5.3
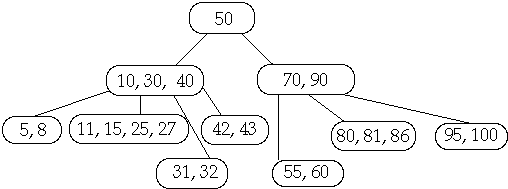
A tree T is a B-Trees of degree t if
a) All leaves of T have the same depth
b) All internal nodes of T except the root we have:
- t<= c(v) <= 2t
c) The root of T satisfies 2 <= c(v) <= 2t
c(v) = number of children of node v
Other Definitions of B-Tree
All internal nodes of T except the root we have:
- t <= c(v) <= 2t
All internal nodes of T except the root have between
- t-1 and 2t-1 keys
All internal nodes of T except the root we have:
- t+1 <= c(v) <= 2t + 1
All internal nodes of T except the root we have:
- t/2 <= c(v) <= t
All internal nodes of T except the root we have:
-
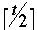 <= c(v) <= t
<= c(v) <= t
Theorem. If n >= 1, then for any n-key B-tree T of height h and
degree t >= 2 then
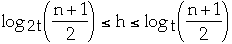
proof.
-
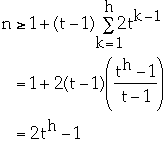
so
-
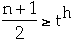
take log of both sides.
How many levels?
| t | N | # of Levels |
| 256 | 33,000,000 | 4 |
| 256 | 8,550,000,000 | 5 |
| | |
| 128 | 4,100,000 | 4 |
| 128 | 530,000,000 | 5 |
Theorem. The worst case search time on a n-key B-tree T of degree t is
O(lg(n)).
- A node in T has t-1 <= K <= 2t-1 keys in sorted order.
-
- Worst case:
- K = t-1 for all nodes
- searching for X not in the tree
-
-
- Given a node, W, in T, how much work does it take to find the subtree of W
that would contain X?
-
- Using binary search it takes
-
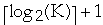 =
=
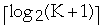 =
=
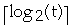 comparisons
comparisons
-
- Since the height of the tree is in worst case
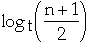 the total amount of work is:
the total amount of work is:
-
-
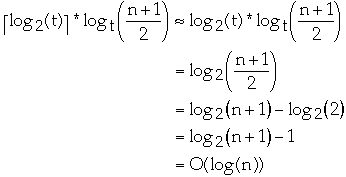
Inserting X into B-tree T of degree t
A full node is one that contains 2t-1 keys
1. Find the leaf that should contain X
2. If the path from the root to the leaf contains a full node, then split the
node when you first search it.
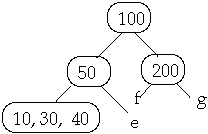
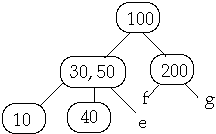
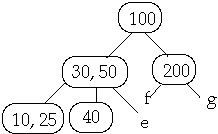
Example t = 2, Insert 25
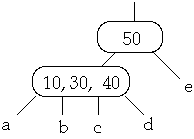 Full Node is split, Then insert 25 into subtree b
Full Node is split, Then insert 25 into subtree b
3. Insert X into the proper leaf
Example t = 2, Insert 25
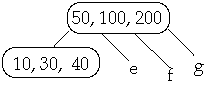
Deleting X from B-tree T of degree t
A minimal node is one that contains t-1 keys and is not the root
In the search path from the root to node containing X, if you come across a
minimal node add a key to it.
Case 3. Searching node W that does not contain X. Let c be the child of W
that would contain X.
Case 3a. if c has t-1 keys and a sibling has t or more keys, steal a key from
the sibling
Example t = 2, Delete 250
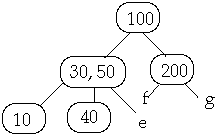
Case 3b. if c has t-1 keys and all siblings have t-1 keys, merge c with a
sibling
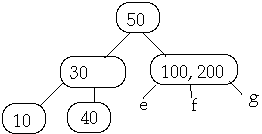
Example 1. t = 2, Delete 250
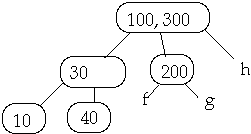
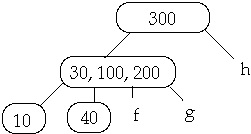 Example 2. t = 2, Delete 250
Example 2. t = 2, Delete 250
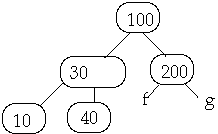
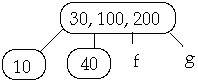
Case 2. Internal node W contains X.
Case 2a. If the child y of W that precedes X in W has at least t keys, steal
predecessor of W
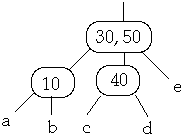
Example 1. t = 2, Delete 50
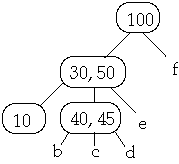 Now Delete 45w
Now Delete 45w
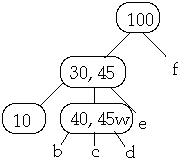
Case 2b. If the child z of W that succeed X in W has at least t keys, steal
the successor of W
Example 1. t = 2, Delete 30
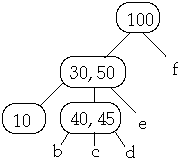 Now Delete 40w
Now Delete 40w
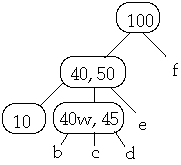
Case 2c. If both children z and y of W that succeed (follow) X in W have only
t-1 keys, merge z and y
Example t = 2, Delete 30
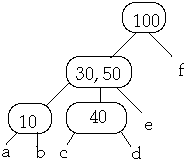 Now Delete 30w one lower level
Now Delete 30w one lower level
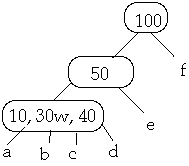
Case 1. X is in node W a leaf. By case 3, W has at least t keys. Remove X
from W
Theorem. A Red-Black tree is a B-Tree with degree 2
proof:
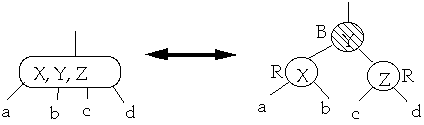
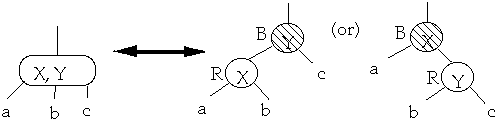
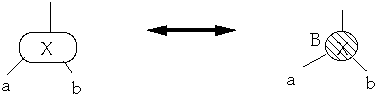
Must show:
-
- 1. If a node is red, then both its children are black
-
- 2. Every simple path from a node to a descendant leaf contains the same
number of black nodes
Leaf-Oriented Storage
Data is stored in leaves. Internal nodes are used to index into leaves.
Node-Oriented Storage
 Leaf-Oriented Storage
Leaf-Oriented Storage
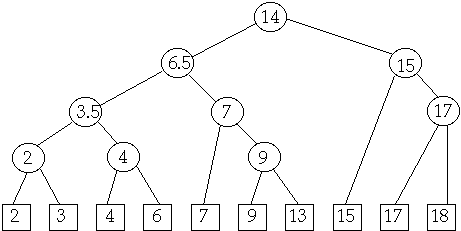
Will assume items of interest are stored in the leafs, but this is not
required
Leaf contains one key
Internal nodes contain keys used to find leafs
Let a and b be integers with a >= 2 and 2a-1 <= b. A tree T is an (a,
b)-tree if
a) All leaves of T have the same depth
b) All internal nodes v of T except the root satisfy a <= c(v) <= b
c) The root of T satisfies 2 <= c(v) <= b
c(v) = number of children of node v
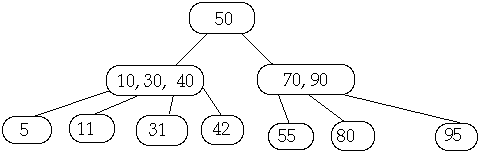
(2, 4) Tree Insert 6
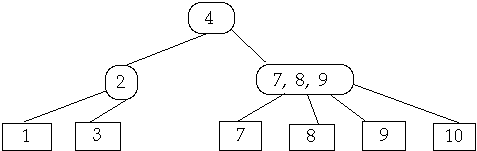 Find Proper Leaf Location and Add
Find Proper Leaf Location and Add
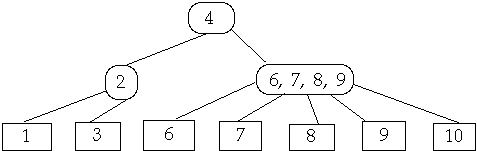 If needed Split Node
If needed Split Node
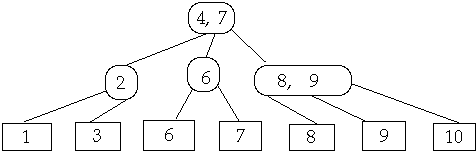
Delete 6
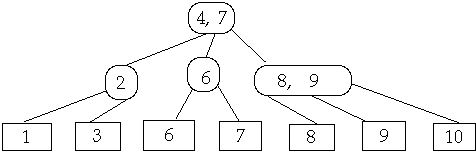 Find and Delete leaf, Shrink Parent
Find and Delete leaf, Shrink Parent
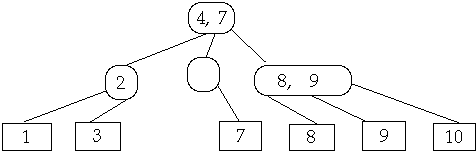 If needed either fuse parent or
If needed either fuse parent or
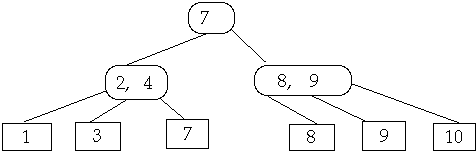
Share nodes from Sibling
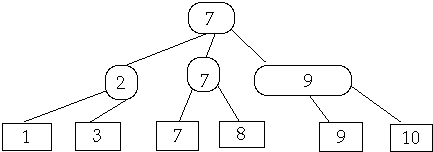
Let T be an ( a, b )-tree with n leaves and height h. Then:
a)
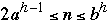
b) lg (n)/lg (b) <= h <= 1 + lg( n/2 ) / log ( a )
Theorem[1] Let b >= 2a and
a >= 2. Perform any sequence of i insertions and d deletions( n = i + d )
into an initially empty ( a, b)-tree. Let
- SP = total number of node splittings
- F = total number of node fusings
- SH = total number of node sharings
then:
SP + F + SH = O( n ).
This is not true when b = 2a - 1. That is for certain definitions of
B-trees!
Values of a and b?
Assume b = 2a
Assume it costs C1 + C2m time units to move m contiguous
elements from secondary to main memory
C1 = latency time, C2 = time to move one storage
location
Assume it costs K1 + K2n to determine the subtree of
interest in a node containing n keys
Total search time in (a , b ) -tree will be bound by
- Time to search one node * number of levels
-
- ( K1 + K2a + C1 + C2a ) lg( n )
/ lg( a )
This is minimal when
- a* ln( a - 1 ) = ( K1 + C1 ) / ( K2 +
C2 )
Tree In Main Memory
K1 ~ K2 ~ C1 and C2 = 0 so a
= 2 or 3
Tree In Secondary Memory
K1 ~ K2 ~ C2 and C1 ~
1000K1 ( in 1983 )
This gives a ~ 100
The Action is Near the Leaves
Let leaves be level 0 ( just for this slide )
Parents of leaves be level 1, ...
Theorem[2] Let b >= 2a and
a >= 2. Perform any sequence of i insertions and d deletions( n = i + d )
into an initially empty ( a, b)-tree. Let
- SPh = total number of node splittings at height h
- Fh = total number of node fusings at height h
- SHh = total number of node sharings at height h
then:
- SPh + SHh + Fh <= 2( c + 2 ) n / (c +
1 ) h
-
where:
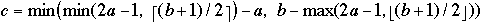
The Action is Near the Leaves - Who Cares?
Concurrent Databases
A = access by a seperate processor
 =node locked as processor changes node
=node locked as processor changes node
AB = access blocked by locked node
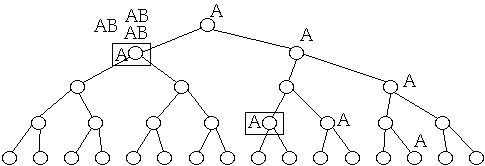
A-Sort
A-sort (next slides) uses the fact that the action is near the leaves
( a, b )-Trees and Sorting
Let x[1], x[2], ..., x[n] be a sequence to be sorted
Let f[k] = | { x[j] : j > k and x[j] < x[k] } |
Let
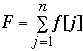
F is the number of inversions of x[1], x[2], ..., x[n]
Example
1 2 7 3 4 5 9 6 8
has
6 inversions
Facts
1) 0 <= F <= N*(N+1)/2 for a list of N items
2) Let F = number of inversions of a list A. Insertion sort takes
-
 (
n + F ) operations to sort A
(
n + F ) operations to sort A
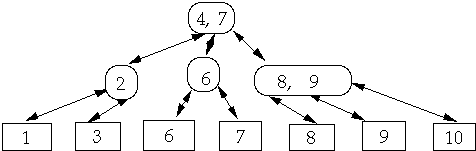
Sort x[1], x[2], ..., x[n] by inserting into a ( a, b )-Tree
Insert x[1], then x[2], then x[3], ... into the tree
When inserting x[k] need to find the proper location for x[k]
Don't start the search at the root
Start the search at the "right most" internal node
This process is called A-sort
Theorem[3] A sequence of n elements with F
inversions can be sorted using A-sort in:
- O( n + n lg( F / n ) )
Theorem[4] A-sort is better than quicksort
for list with number of inversion F <= 0.02N1.57
 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
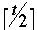 <= c(v) <= t
<= c(v) <= t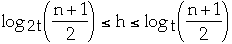
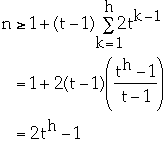
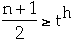
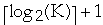 =
=
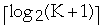 =
=
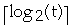 comparisons
comparisons
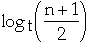 the total amount of work is:
the total amount of work is:
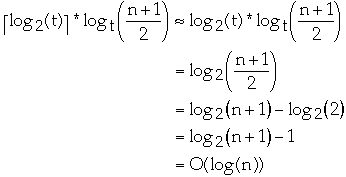


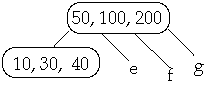








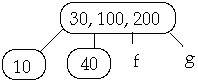






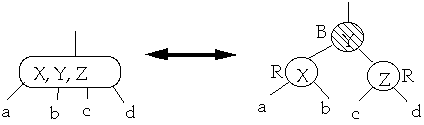












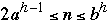
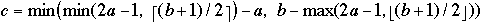
 =node locked as processor changes node
=node locked as processor changes node
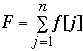
 (
n + F ) operations to sort A
(
n + F ) operations to sort A