CS660 Combinatorial Algorithms
Fall Semester, 1996
Amortized Analysis
[To Lecture Notes Index]
San Diego State University -- This page last updated Thursday, 19 September, 1996
Contents of Amortized Analysis
- Reference
- Amortized Analysis
- Aggregate Method
- Accounting Method
- Potential Method
Introduction to Algorithms by Cormen, Leiserson, Rivest. Chapter 18
Dynamic Array
When an array becomes full, just copy the array elements to a larger
array
Array-> pointer to an array
Number -> number of items in the array
Size -> size of the array
AddToTable(x)
if Number == Size then
allocate NewArray with size 2*Size
insert all items from Table to NewArray
free Array
Array= NewArray
Size = 2 * Size
end if
insert x into Array
Number = Number + 1
end insert
In a sequence of operations on a data structure often the worst case can not
occur in each operation
The worst case cost of inserting an element in a dynamic array is N + 1
N = size of the array before the insertion
But you can't get two worst cases in a row!
Amortized Analysis gives the average performance of each operation in
the worst case
Three methods used in amortized analysis
- Aggregate Method
-
- Accounting Method
-
- Potential Method
Example - Incrementing a k-bit binary counter
Let A[0..k-1] be an array of bits representing a number X
A[0] - low order bit, so
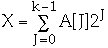
length[A] = k
Start with X = 0
Increment (A)
J = 0
while J < length[A] and A[J] == 1 do
A[J] = 0
J = J + 1
end while
if J < length[A] then
A[J] = 1
end if
end Increment
Count bits flipped
Worst Case
- Increment flips k bits in worst case
-
- Sequence of n Increment operations takes O(nk)
T(n) = all work done in worst case in sequence of n operations
Amortized cost per operation is T(n)/n
| X | A[4] | A[3] | A[2] | A[1] | A[0] | Total Cost |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 2 | 0 | 0 | 0 | 1 | 0 | 3 |
| 3 | 0 | 0 | 0 | 1 | 1 | 4 |
| 4 | 0 | 0 | 1 | 0 | 0 | 7 |
| 5 | 0 | 0 | 1 | 0 | 1 | 8 |
| 6 | 0 | 0 | 1 | 1 | 0 | 10 |
| 7 | 0 | 0 | 1 | 1 | 1 | 11 |
| 8 | 0 | 1 | 0 | 0 | 0 | 15 |
| 9 | 0 | 1 | 0 | 0 | 1 | 16 |
A[0] flips each time Increment is called n
A[1] flips every other time
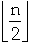
A[1] flips every fourth time
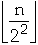
A[J] flips every 2J time
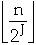
Total number of flips is:
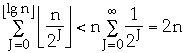
So amortized cost of each operation is 2 = O(1)
Assign an amortized cost to each operation
Amortized cost may be more or less than the actual cost
If amortized cost is more than the actual cost of the operation assign the
difference to part of the data structure as a credit
No negative credit allowed
Total amortized cost is >= total worst case cost
Example - binary counter
Amortized cost of setting bit to 1 2 units
- 1 unit to pay for setting bit to 1
-
- 1 unit stored with bit
Amortized cost of setting bit to 0 0 units
- Only a 1-bit is set to 0,
-
- All 1-bits have credit of one unit
-
- This pays for setting bit to 0
Example Continued
Increment (A)
J = 0
while J < length[A] and A[J] == 1 do
A[J] = 0 Cost 0
J = J + 1
end while
if J < length[A] then
A[J] = 1 Cost 2
end if
end Increment
| X | A[4] | A[3] | A[2] | A[1] | A[0] | Amortized cost |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 (1) | 2 |
| 2 | 0 | 0 | 0 | 1 (1) | 0 | 4 |
| 3 | 0 | 0 | 0 | 1 (1) | 1 (1) | 6 |
| 4 | 0 | 0 | 1 (1) | 0 | 0 | 8 |
| 5 | 0 | 0 | 1 (1) | 0 | 1 (1) | 10 |
| 6 | 0 | 0 | 1 (1) | 1 (1) | 0 | 12 |
| 7 | 0 | 0 | 1 (1) | 1 (1) | 1 (1) | 14 |
| 8 | 0 | 1 (1) | 0 | 0 | 0 | 16 |
| 9 | 0 | 1 (1) | 0 | 0 | 1 (1) | 18 |
Assign an amortized cost to each operation
Amortized cost may be more or less than the actual cost
If amortized cost is more than the actual cost of the operation assign the
difference the entire data structure as potential energy
ck= actual cost of operation k
=
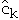amortized cost of operation k
Dk = the state of the data structure after applying k'th operation to Dk
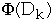= potential associated with Dk
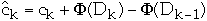
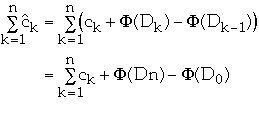
So if
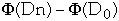>=0
then
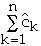is an upper bound on total cost of the algorithm
Example - binary counter
Potential = number of 1's in the counter
if the k'th operation sets
bits to 0 the actual cost is
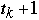
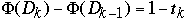
so
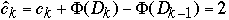
How to find
?
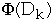Dynamic Tables
Table -> pointer to a table
Number -> number of items in the table
Size -> size of the table
AddToTable(x)
- if Number == Size then
-
- allocate NewTable with size 2*Size
-
- insert all items from Table to newTable
-
- free Table
-
- Table = NewTable
-
- Size = 2 * Size
- end if
-
- insert x into Table
-
- Number = Number + 1
end insert
How many inserts are done by N AddToTable?
Amortized Cost per AddToTable 3 inserts
Table after moving from size 4 to size 8
Perform 4 AddToTable operations
| X | X | X | X | | | | | | | | |
|
| X | X | X | X | Y(2) | | | | | | |
|
| X | X | X | X | Y(2) | Y(2) | | | | |
|
| X | X | X | X | Y(2) | Y(2) | Y(2) | | |
|
| X | X | X | X | Y(2) | Y(2) | Y(2) | Y(2) |
1/2 the table has 2 credits
One credit per item to pay for the move to next size table
Table Expansion and Contraction
Policy
- When table becomes full move to table twice the size
-
- When table contracts to 1/4 full, move to table 1/2 size
Let load = (Size of table) / (number of items in the table)
Amortized Cost
- Inserting when load >= 1/2
- 3 units
-
- Inserting when load < 1/2
- 0 units
-
- Deleting when load > 1/2
- 0 units
-
- Deleting when load <= 1/2
- 2 units
| X | X | X | X | | | | | | | | |
| X | X | X | X | Y(2) | | | | | | |
| X | X | X | X | | | | | | | | |
| X | X | X | (1) | | | | | | | | |
| X | X | (1) | (1) | | | | | | | | |
| X | X | | | | | | | | |
Linked List vs. Dynamic Array
Unordered List
Amortized Costs per operation over n operations
| linked List | Dynamic Array |
| | |
| Insertion | 1 call to new | lg(n)/n call to new |
| | |
| set two links | 3 data moves |
| Deletion | two links | 3 data moves |
| after find | | |
| 1 delete | lg(n)/n call to delete |