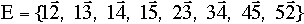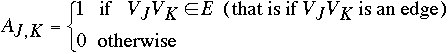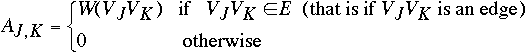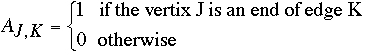CS660 Combinatorial Algorithms
Fall Semester, 1996
Basic Graphs
[To Lecture Notes Index]
San Diego State University -- This page last updated Nov 19, 1996
Contents of Basic Graphs
- References
- Definitions
- Graph
- Digraph
- Subgraph
- Complete Graph
- Path
- Adjacent Vertices
- Connected Graph
- Cycle
- Simple Cycle
- Weighted Graph
- Representation of Graphs
- List of edges
- Adjacency Matrix
- Adjacency list
- Incidence Matrix
- Traversing Graphs
- Breath-first(Graph, startNode)
- Depth-first(Graph, startNode)
- Minimal Spanning Tree
- Minimal Spanning tree Prim
Chapters 23 and 24 of text.
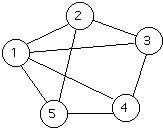
A graph G is a pair (V,E) where
- V is a set of vertices (or nodes)
-
- E is a set of edges connecting the vertices
-
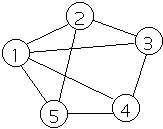
EXAMPLE
- V = {1,2,3,4,5}
-
- E = {(1,2), (1,3), (1,4), (1,5), (2,3), (3,4), (4,5),(5,2)}
A Digraph is a graph in which each edges has a direction.
EXAMPLE
- V = { 1,2,3,4,5}
-
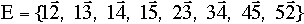
A Subgraph G'= (E',V') of a graph G = (E,V) is a graph where V' is a subset of
V and E' is a subset of E
A graph with an edge between each pair of vertices
Note for any G = (E,V) we have 0 <= |E| <= |V|*(|V|-1)/2
A path in a graph from vertex V to vertex W is a sequence of edges
(V1,V2), (V2,V3),...
(Vk-2,Vk-1), (Vk-1,Vk) such that V
= V1, and W = Vk. The path is usually given as
V1,V2,V3,...Vk
The above path has length k.
Two vertices are adjacent if there is an edge connecting them
A graph is connected if there is a path between any two vertices
A path starting and ending on the same vertex
A cycle in which all vertices are visited exactly once except the starting
vertex: which is visited only twice
A weighted graph G = (V,E,W) is a graph where each edge e in E has a weight
denoted by W(e)
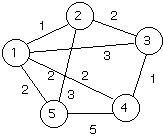
The weight of a Graph is the sum of the weights of the edges of the graph
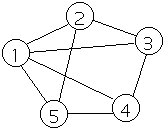
EXAMPLE
- 1, 2
- 1, 3
- 1, 4
- 1, 5
- 2, 3
- 3, 4
- 4, 5
- 5, 2
Space - O(|E|) ( actually 2|E|)
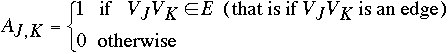
| 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 1 | 0 |
| 4 | 1 | 0 | 1 | 0 | 1 |
| 5 | 1 | 1 | 0 | 1 | 0 |
Space - O(|V|2) (can be ~ |V|2/2)
For weighted graph
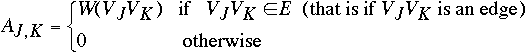
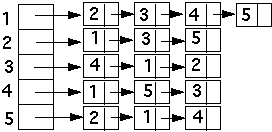
Space - O(|E| + |V|)
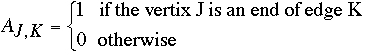
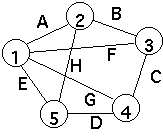
| A | B | C | D | E | F | G | H |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 5 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
Space - O(|E|*|V|)
Line number
for X := 1 to |V| do 1
Type[X] := unvisited; 2
Create(Queue); 3
Type[startNode] := inQueue 4
Insert(startNode, Queue); 5
visitOrder := 1; 6
while not IsEmpty(Queue) do 7
nextNode := GetFirst(Queue); 8
List[nextNode] := visitOrder; 9
visitOrder := visitOrder + 1; 10
Type[nextNode] = visited; 11
for each node adjacent to nextNode do 12
if Type[node] = unvisited then 13
Type[node] := inQueue; 14
Insert(node, Queue); 15
end if;
end for;
end while;
return List
Analysis of Breath-First Search
Measure of size of input: |E| and |V|
Structures used:
Type
- array of size |V|
- Each element changed at most three times:
- random -> unvisited -> inQueue -> visited
List
- array of size |V|
- Each element changed once
Queue
- Contains at most |V| - 1 elements
- At most |V| adds and |V| deletes from queue
- At most |V| calls to IsEmpty
VisitOrder
- Increased |V| times
Analysis of Breath-First Search - Cont.
Graph
Must find all neighbors of each node in graph
Adjacency Matrix O(|V|2)
| 1 | 2 | 3 | 4 | 5 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 2 | 1 | 0 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 1 | 0 |
| 4 | 1 | 0 | 1 | 0 | 1 |
| 5 | 1 | 1 | 0 | 1 | 0 |
Adjacency list O(|E| + |V|)
-
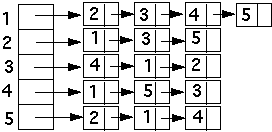
Traversing Graphs
Line number
for X := 1 to |V| do 1
Type[X] := unvisited; 2
Create(Stack); 3
Type[startNode] := inStack; 4
Insert(startNode, Stack); 5
visitOrder := 1; 6
while not IsEmpty(Stack) do 7
nextNode := Pop(Stack); 8
List[nextNode] := visitOrder; 9
visitOrder := visitOrder + 1; 10
Type[nextNode] = visited; 11
for each node adjacent to nextNode do 12
if Type[node] = unvisited then 13
Type[node] := inStack; 14
Push(node, Stack); 15
end if;
end for;
end while;
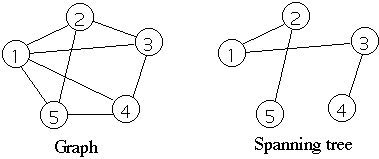
Spanning tree of a graph G
A subgraph of G that is a tree and contains all vertices of G
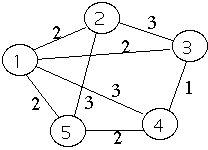
Minimal Spanning tree of a weighted graph
The spanning tree with the least weight
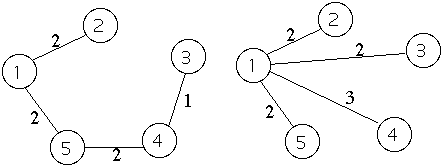
Notation For Algorithm
V1 - vertices that are part of the spanning tree already
E1 - edges in spanning tree
V2 - vertices not in V1 but adjacent to a vertex in
V1
E2 - for each vertex y in V2, E2 contains
the edge of minimal weight connecting y to a vertex in V1
V3 - all remaining edges
E3 - all remaining vertices
Theorem Basis of Algorithm
Let G=(V,E,W) be a weighted graph with weights in Z+. Let
E1 be a subset of edges in some minimal spanning tree T of G. If xy
is an edge of minimal weight with x in V1 and y not in V1
then E1 + {xy} is a subset of a minimal spanning tree.
Outline of Algorithm
1) Initialize the sets
V1 = {x}, E1, E2, V2 = empty set, V3 = V - V1
2) while V1 != V do
for each y in V2 adjacent to x do
find shortest edge from y to element in V1
add edge to E2
end for
for each w in V3 adjacent to x do
add w to V2
add wx to E2
end for
if E2 is empty then return 'no spanning tree'
find edge zv in E2 with minimum weight
z in V1 , v in V2
add v to V1, remove zv from E2
end while
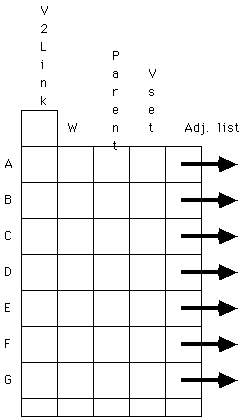
Data structures for MSP algorithm
for each vertex we need:
-
- a) an adjacency list
-
- b) the set (V1,V2,V3) the vertex is in
-
- c) the edge in E2 if any for the vertex
-
- d) The edge connecting the vertex to the spanning tree
We also need a list of the vertices in the set V2.
