 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms
Fall Semester, 1996
Intro to Trees
[To Lecture Notes Index]
San Diego State University -- This page last updated Sep 26, 1996

Contents of Intro to Trees
- References
- Dictionary
- Tree Operations on BST
- Tree Operations - Performance
- General Terms
Introduction to Algorithms by Cormen, Leiserson, Rivest. Chapter 13
Data Structures and Algorithms 1: Sorting and Searching, Mehlhorn, Kurt,
pages 174-177
Basic Operations
Access (k, t): Return the item in dictionary t with key k; if no item in t has
key k, return null
Insert (j, t): Insert item j into t, not previously containing j
Delete (j, t): Delete item j from t
Operations based on order
Minimum (t): Return the item in t with the smallest key
Maximum (t): Return the item in t with the largest key
Successor (k, t): Return the item in t with the smallest key larger than k
Predecessor (k, t): Return the item in t with the largest key smaller than k
Multiple-Structure Operations
Join (a, i, b): Return dictionary formed by combining dictionary a, item i, and
dictionary b. Assumes that every item in a has key less then key(i) and every
item in b has key larger than key(i)
Split (i, s): Split dictionary s, containing item i, into three dictionarys:
a, containing all items with key less than key(i); single dictionary i; and b,
containing all items with key greater than key(i)
Types of Structures & Algorithms for Dictionaries
Lists in arrays, unordered
Lists in arrays, ordered
Linked Lists, unordered
Linked Lists, ordered
Hash tables
Binary trees
Skip Lists
B-Trees
Heaps
What are the advantages of each?
Types of Algorithms for Trees
Off-line
- Totally balanced BST
- Know all items in list
-
- Minimize worst case search
-
- Optimum BST
-
- Know all items and probability of access
-
- Minimize total search cost over all access
On-line
- Balanced BST (Weight, Height), Skip lists
-
- Add items as they show up
-
- Minimize worst case search
-
- Self-Adjusting BST
- Modify tree based on access pattern
Access, Minimum, Maximum, Successor, Predecessor, Insert
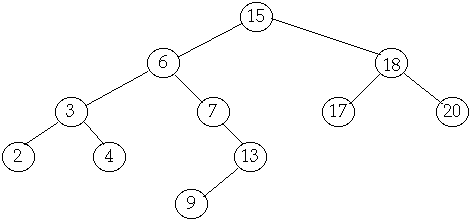
Tree Operations
Delete
Case
1 Delete leaf
Delete(20)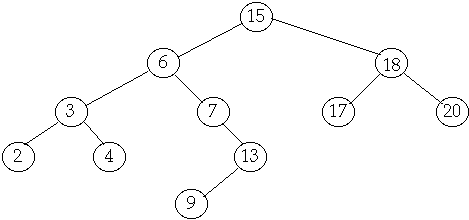
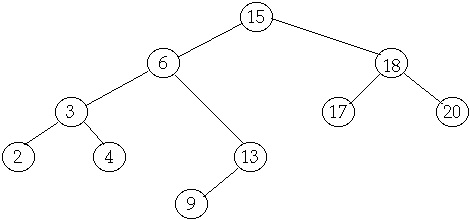
Tree Operations
Delete
Case
2 Delete node with one child
Delete(7)
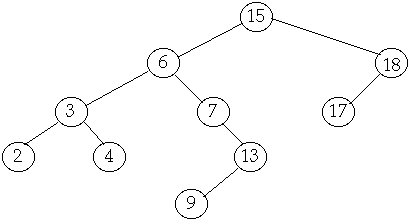
Tree Operations
Delete
Case
3 Delete node with two children
Delete(6)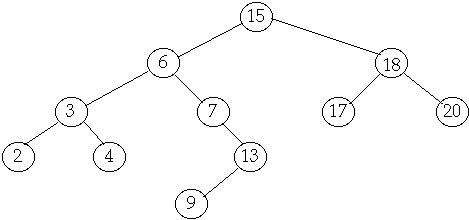
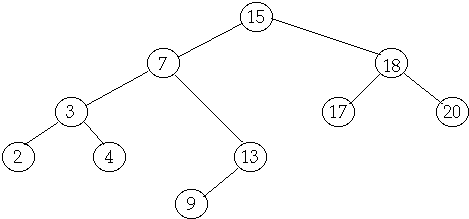
Theorem
- The operations Access, Minimum, Maximum, Successor, Predecessor, Insert,
and delete run in O(h) on a BST of height h
Randomly Built BST
Assume that we have n distinct keys in random order
Each n! permutations of the input keys is equally likely
Insert the keys in an empty tree, using random order
Theorem
- The average height of a randomly built BST on n distinct keys is O( lgn
)
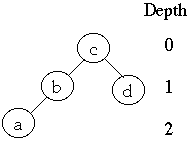
We have a list of n items: a1, a2, ..., an
in BST
Probability of accessing item ak is P(ak) =
Alphak
Let Betak be the probability of accessing a key
that is between ak and ak+1
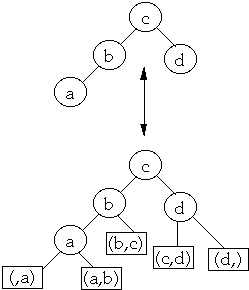
More Terms
Let bk be the leaf between ak and ak+1
Betak is the probability of accessing leaf bk
Ordered by keys we have , b0< a1 <b1<
a2 < ... < an < bn
(Beta0 ,Alpha1 ,Beta1 ,
Alpha2, Beta2,... ,
Alphan, Betan)1 is called the
access distribution
Let

Weighted path length of a tree
Let D(ak) = depth of node ak
Define the weighted path length of tree T as:
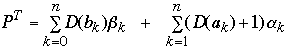
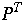 is the average number of comparisons in a search of T
is the average number of comparisons in a search of T
Entropy
Let (Gamma1 ,Gamma2,... ,
Gamman) be a discrete probability distribution, i.e.
Gammak >= 0 and SigmaGammak
=1
H(Gamma1 ,Gamma2,... ,
Gamman) =
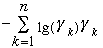
is the entropy of the distribution.
Use the convention that 0*lg 0 = 0
| Gamma1 | Gamma2 | Gamma3 | Gamma4 | Gamma5 | Gamma6 | Gamma7 | Gamma8 | H |
| .125 | .125 | .125 | .125 | .125 | .125 | .125 | .125 | 3 |
| .250 | .250 | .250 | .250 | .000 | .000 | .000 | .000 | 2 |
| .500 | .500 | .000 | .000 | .000 | .000 | .000 | .000 | 1 |
| 1.000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | 0 |
| .900 | .010 | .010 | .010 | .010 | .010 | .010 | .010 | .602 |
| .800 | .160 | .032 | .0064 | .00128 | .00026 | .00005 | .00001 | .902 |
| .368 | .184 | .123 | .092 | .074 | .061 | .053 | .046 | .265 |
Lower bound on weighted Path Length
We have a list of n items: a1, a2, ..., an
in BST
Probability of accessing item ak is P(ak) =
Alphak
Let bk be the leaf between ak and
ak+1
Betak is the probability of accessing leaf bk
Let
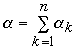
H = H(Beta0 ,Alpha1
,Beta1 , Alpha2,
Beta2,... , Alphan,
Betan)
P =
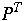
Theorem 5[2] For any BST we have:
- a)
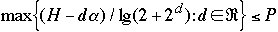
-
- b)
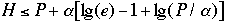
 CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms CS660 Combinatorial Algorithms
CS660 Combinatorial Algorithms