 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Networks part 2
[To Lecture Notes Index]
San Diego State University -- This page last updated April 16, 1996

Contents of Networks part 2 Lecture
- Embedding Networks
- Embedding a Linear Array onto a Hypercube
- Embedding a Mesh into a Hypercube
- Hypercube and Binary Search Trees
- Butterfly Network
Broadcast on Hypercube
for Id = 0 to  do in parallel
for stage = 0 to d do
partner := Id XOR
do in parallel
for stage = 0 to d do
partner := Id XOR  if haveMessage is true then send message to partner
if partnerMessageQueue is not empty then read message
end for
end for
if haveMessage is true then send message to partner
if partnerMessageQueue is not empty then read message
end for
end for

Scan on Hypercube
Assume each processor starts with a value stored in myNumber
for Id = 0 to  do in parallel
result := myNumber
message := result
for stage = 0 to d do
partner := Id XOR
do in parallel
result := myNumber
message := result
for stage = 0 to d do
partner := Id XOR  send message to partner
receive number from partner
message := message + number
if ( partner < Id ) then result := result + number
end for
end for
send message to partner
receive number from partner
message := message + number
if ( partner < Id ) then result := result + number
end for
end for

Let G( V, E) and G'( V', E' ) be graphs
- V, V' are set of vertices
-
- E, E' are set of edges
A map H: G -> G' is an embedding if:
- each vertex in V is mapped to a vertex in V'
-
- and each edge in E is mapped to one or more edges in E'
Congestion
- Maximum number of edges of E mapped on to any edge in E'
Dilation
- Maximum number of edges of E' that any one edge of E is mapped onto
-
- That is how much we stretch an edge of E
Expansion
- |V' |/| V|
Load
- Maximum number of vertices of E that are mapped to a single vertex of
E'
Embed a linear array of
 processors into d-dimensional Hypercube
processors into d-dimensional Hypercube
1. Label the processors of the linear array in order from 0 to
 -1
-1

2. Map linear array processor K to processor H( i, d) where:
- H( 0, 1 ) = 0
- H( 1, 1 ) = 1
-
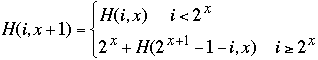
The sequence generated by the H's is a Gray code
Gray Codes - The Easy Way
1-bit code is 0 then 1
To get x-bit code:
-
- copy (x-1)-bit code, call it A
-
- repeat the (x-1)-bit code in reverse order, call it B
-
- add a 0 bit in front of the elements of A
-
- add a 1 bit in front of the elements of B

Sample Embedding

| Congestion | 1 |
| Dilation | 1 |
| Expansion | 1 |
| Load | 1 |
A
 mesh can be embedded into a s+r dimensional hypercube with dilation and
congestion 1
mesh can be embedded into a s+r dimensional hypercube with dilation and
congestion 1
proof:
1. Label the mesh using 2 dimensional coordinates

2. Produce gray code for each dimension
| Number | Gray Code |
| 0 | 00 |
| 1 | 01 |
| 2 | 11 |
| 3 | 10 |
3. Concatenate gray codes to produce gray code for tuples
| Tuple | Gray Code |
| (0,0) | 0 00 |
| (0,1) | 0 01 |
| (0,2) | 0 11 |
| (0,3) | 0 10 |
| (1,0) | 1 00 |
| (1,1) | 1 01 |
| (1,2) | 1 11 |
| (1,3) | 1 10 |
4. Gray code indicates the processor in the Hypercube the mesh processor will be mapped onto

 Theorem
Theorem
- A
 mesh can be embedded into a
mesh can be embedded into a
 -dimensional
hypercube with dilation and congestion 1
-dimensional
hypercube with dilation and congestion 1
A complete binary search tree is a binary search tree such that:
-
- All internal nodes have two children, with one possible exception
-
- All leaves occur on at most two different, but consecutive, levels
-
- If a level contains leaves and internal nodes, the internal nodes must be
to the left of all leaves, internal nodes with two children must be to the left
of internal nodes with one child

Theorem
- A complete binary search tree with
 nodes can not be embedded into a r-dimensional hypercube with dilation and
congestion 1 when r > 2
nodes can not be embedded into a r-dimensional hypercube with dilation and
congestion 1 when r > 2
proof:
- Assume you can and the root of the tree is mapped to node 0 in the hypercube
-
- Label the nodes in the hypercube either even or odd, depending on the sum
of the bits of the processor number
-
- There will be
 odd nodes and
odd nodes and
 even nodes
even nodes

- Label the nodes in the tree even or odd, depending on which type of node it
is mapped to in the hypercube
-
- All nodes on the same level will have the same label
 Lemma
Lemma
- A complete binary search tree with
 nodes has
nodes has
 leaves
leaves
proof:

Back to proof of theorem
Let X be the polarity (odd or even )of the lowest level
If there are more than 2 levels, there will be at least
 +1
nodes of polarity X
+1
nodes of polarity X
But an r-dimensional hypercube does not have
 +1
nodes of the same polarity
+1
nodes of the same polarity
The r-dimensional butterfly has
 nodes and
nodes and
 edges
edges
Processors (nodes) are labeled as (w, i ) where:
- i denotes the level or dimension of the processor
-
- 0 <= i <= r
-
- w is an r-bit binary number that denotes the row of the processor
Two processors (w, i ) and (w', i' ) are connected if and only if
- i' = i + 1 and either
- w = w' ( straight edge )
-
- w and w' differ in the i'th bit ( cross edge )
Three-Dimensional Butterfly

Butterfly and Hypercube
The hypercube is a folded up butterfly
The k'th row of the butterfly corresponds to the k'th processor in the
hypercube
The k'th dimensional edge (u, v) of the hypercube corresponds to the cross
edges (<u, k-1>, <v,k>) and (<v,k-1>, <u,k>)




 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithmsdo in parallel for stage = 0 to d do partner := Id XOR
if haveMessage is true then send message to partner if partnerMessageQueue is not empty then read message end for end for
do in parallel result := myNumber message := result for stage = 0 to d do partner := Id XOR
send message to partner receive number from partner message := message + number if ( partner < Id ) then result := result + number end for end for