SDSU CS 662 Theory of Parallel Algorithms
Numerical Methods 1

[To Lecture Notes Index]
San Diego State University -- This page last updated April 25, 1996
----------

Contents of Numerical Methods 1 Lecture

  1. Numerical Algorithms
    1. Matrix Algorithms
      1. Transposition
      2. Matrix Multiplication

Numerical Algorithms


Basic Issue - Digital computers don't do math (like math books)
may not the same as
may not be the same as


Problem 1. Errors

Let c = a = and let b=

What is ?

What is ?
Problem 2. Computational Complexity

Computing requires n multiplications

So computing requires
2n multiplications and n additions


But requires
n multiplications and n additions

Compute
Method 1



Requires n multiplications
Method 2

Let

Algorithm
Result = x
for k = 1 to r do
Result = Result * Result

Requires log(n) multiplications


Let n be any value

Let be the binary representation of n

Then

So

but in log(n) multiplications we can compute all the terms

It takes another log(n) multiplications to multiply them together


Problem 3

It can take more human effort and some deep mathematics to perform numerical analysis

Matrix Algorithms

Transposition


Let A be an n*n matrix, for example

The transpose, , of A is obtained by mapping for all j and k

Computing from A sequentially by:
for j = 2 to n do
	for k = 1 to j - 1 do
		temp = A[ j, k ]
		A[ j, k ] = A[ k, j ]
		A[ k, j ] = temp 
	end for
end for

Time Complexity = O(n*n)
EREW Transpose

Use (n*n - n)/2 processors
for j = 2 to n do in parallel 
	for k = 1 to j - 1 do in parallel 
		Processor P(j, k) 
			temp = A[ j, k ]
			A[ j, k ] = A[ k, j ]
			A[ k, j ] = temp 
	end for
end for


Time Complexity = O( 1 )
Cost = n*n



Big Deal!What about Networks?
Transpose on Shuffle-Exchange

Let n = and use shuffle-exchange network with processors

Map elements of A to the processors by:
where for j, k = 1 to n
Note:
(j-1) and (k-1) range from 0 to n-1
(j-1) and (k-1) take r bits to store

So can be obtained by writing the bits of ( j - 1) then following them with the bits of (k-1).
Algorithm

Shuffle r times
Example 1

Let r = 1 so n = 2

We have and

Map to the 4 node shuffle-exchange network

Now perform 1 shuffle on all nodes
Example 2

Let r = 2 so n = 4
We have ,

map to the 16 node shuffle exchange network

now perform 2 shuffles

Matrix Multiplication


Let A be an n*n matrix, and x be a vector with n elements

Compute y = Ax
We have
Matrix-Vector Multiplication on Linear Array
Matrix Matrix Multiplication

Let A and B be a n*n matrices

Compute C = A*B

We have

This requires n multiplications and n-1 additions per element of C

So it takes multiplications and 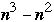additions to compute C
Matrix-Matrix Multiplication on Linear Array
----------