 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms
Scan
[To Lecture Notes Index]
San Diego State University -- This page last updated March 5, 1996, 1996

Contents of Scan Lecture
- References
- Prefix Sums or Scan Operator
- Prescan Operator
- Generalized Scan
- Scan and Recurrences
- First-Order and Scan
- Higher Order Recurrences
Akl text, chapter 2.5
Guy Blelloch, Prefix Sums and Their Applications. In Synthesis of Parallel
Algorithms ed John Reif, Morgan Kaufmann, 1993, pp 35-60
Let B[K] = A[1] + A[2] + ... + A[K] for K = 1, ..., N
B[] is the prefix sum or +-scan of A[]
procedure AllSums(A[1:N])
for J = 0 to lg(N) - 1 do
for K = 2J + 1 to N do in parallel
Processor Pk: A[K] := A[K- 2J] + A[K]
end for
end for
Time Complexity [[Theta]](lg(N))
Cost [[Theta]]( N*Lg(N) )
How do we know AllSums works?
Use loop invariant for outer loop
Using Fewer Processors
procedure up-sweep(A[1:N])
for d = 0 to lg(N) -1
in parallel for k = 0 to N -1 by 2(d+1)
A[k + 2(d+1) ] = A[k + 2(d+1)] + A[k + 2d]
end in parallel
end for
end up-sweep
procedure down-sweep(A[1:N])
for d = lg(N) - 2 downto 0
in parallel for k = 2(d+1) to N -1 by 2(d+1)
A[k + 2d ] = A[k + 2d] + A[k]
end in parallel
end for
end down-sweep
procedure +-scan(A[1:N])
up-sweep(A)
down-sweep(A)
end +-scan
Scan for any N
procedure up-sweep(A)
for d = 0 to floor(lg(N) -1)
in parallel for k = 0 to N -1 by 2(d+1)
if k + 2(d+1) - 1 < N then
A[k + 2(d+1) ] = A[k + 2(d+1) ] + A[k + 2d]
end in parallel
end for
end up-sweep
procedure down-sweep(A)
for d = floor(lg(N) - 1) downto 0
in parallel for k = 2(d+1) to N -1 by 2(d+1)
if k + 2d - 1 < N then
A[k + 2d ] = A[k + 2d ] + A[k]
end in parallel
end for
end down-sweep
Let B[K] = A[1] + A[2] + ... + A[K-1] for K = 2, ..., N
And B[1] = 0
B[] is the +-prescan of A[]
procedure down-sweep-for-prescan(A[1:N])
A[N] = 0
for d = lg(N) - 1 downto 0
in parallel for k = 0 to N -1 by 2(d+1)
temp = A[k + 2d]
A[k + 2d] = A[k + 2d+1 ]
A[k + 2d+1 ] = A[k + 2d+1] + temp
end in parallel
end for
end down-sweep-for-prescan
procedure +-prescan(A[1:N])
up-sweep(A)
down-sweep-for-prescan(A)
end +-prescan
Applying the slow down principle
Scan
Let N be any integer, P < N
for I = 1 to P do in Parallel
Processor I:
B[I] = 0;
for K = 1 to N/P do
B[I] = A[{(I-1)*N/P}+K] + B[I]
end for
end for
+-prescan(B)
for I = 1 to P do in Parallel
Processor I:
for K = 1 to N/P do
A[{(I-1)*N/P}+K] = A[{(I-1)*N/P}+K] + B[I]
end for
end for
Let @ be a binary associative operation
- a @ (b @ c) = (a @ b) @ c
-
Let B[K] = A[1] @ A[2] @ ... @ A[K] for K = 1, ..., N
B[] is the @-scan of A[]
Let @ be:
- max
-
- min
-
- copy(a, b) {return a}
Let Xk = X(k-1)@A[K] for K > 1
- X1 = A[1]
If @ is a binary associative operation then
- Xk= A[1] @ A[2] @ ... @ A[K]
So simple recurrences can be solve using the scan operator!
First-Order Recurrence
Let Xk = ( X(k-1)*A[K] ) + B[K] for K > 1
- X1 = A[1]
New Binary Operator
If C = [Cl , Cr ] and D = [Dl , Dr ] then define @ operator by:
- C @ D = [Cl * Dl , ( Cr* Dl ) + Dr]
Lemma 1
- @ as defined above is a binary associative operation
proof:
- Must show that (C @ D) @ E = C @ (D @ E)
-
- We have:
-
- (C @ D) @ E = [Cl * Dl , ( Cr* Dl ) + Dr] @ E
- = [Cl * Dl * El , {( Cr* Dl ) + Dr} * El + Er]
-
- = [Cl * Dl * El , Cr* Dl * El + Dr * El + Er]
-
-
- We also have:
-
- C @ (D @ E) =C @ [Dl * El , ( Dr* El ) + Er]
- = [Cl * Dl * El , (Cr * {Dl * El} + ( Dr* El ) + Er]
-
- = [Cl * Dl * El , Cr* Dl * El + Dr * El + Er]
Let Xk = ( X(k-1)*A[K] ) + B[K] for K > 1
- X1 = A[1]
-
- Yk = Y(k-1)*A[K]
- for K > 1, Y1 = A[1]
-
- Sk = [Yk , Xk]
- for K = 1, 2, ...
-
- Ck = [ A[K], B[K] ]
Lemma 2
- Sk = S(k-1) @ Ck for K > 1
proof:
-
- S(k-1) @ Ck = [Y(k-1) , X(k-1)] @ [ A[K], B[K] ]
- = [Y(k-1) * A[K], (X(k-1) * A[K]) + B[K] ]
-
- = [Yk, Xk]
-
- = Sk
Let
-
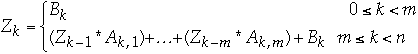
and
-
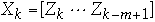
Then we have
-

Thus higher order recurrences can be reduced to a first order
Since scan can solve a first order recurrence, it can solve higher order
recurrences


 CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms CS 662 Theory of Parallel Algorithms
CS 662 Theory of Parallel Algorithms